早教吧作业答案频道 -->数学-->
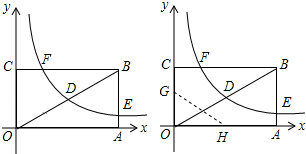
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点F是边BC上的一个动点(不与点B,C重合),过点F的反比例函数y=kx(x>0)的图象与边AB交于点E(4,n),AB=2.(1)若点D为对角线OB的中
题目详情
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点F是边BC上的一个动点(不与点B,C重合),过点F的反比例函数y=
(x>0)的图象与边AB交于点E(4,n),AB=2.
(1)若点D为对角线OB的中点,反比例函数在第一象限内的图象又经过点D.
①求反比例函数的解析式和n的值;
②将矩形OABC折叠,使点O与点F重合,折痕分别与x,y轴正半轴交于点H,G,求线段OG的长.
(2)连接EF,OE,当点F运动到什么位置时,四边形OCFE的面积最大,其最大值为多少?
| k |
| x |
(1)若点D为对角线OB的中点,反比例函数在第一象限内的图象又经过点D.
①求反比例函数的解析式和n的值;
②将矩形OABC折叠,使点O与点F重合,折痕分别与x,y轴正半轴交于点H,G,求线段OG的长.
(2)连接EF,OE,当点F运动到什么位置时,四边形OCFE的面积最大,其最大值为多少?

▼优质解答
答案和解析
(1)①∵D为OB中点,B(4,2),
∴D(2,1),
把D(2,1)代入y=
中,得1=
,即k=2,
∴反比例函数解析式为y=
,
把E(4,n)代入反比例解析式得:n=
=
;
②由F(1,2),得到CF=1,
由折叠得:△OGH≌△FGH,
∴OG=FG,
∵OC=AB=2,
设OG=FG=x,得到CG=2-x,
在Rt△CFG中,由勾股定理得:FG2=CG2+CF2,即x2=(2-x)2+1,
整理得:4x=5,
解得:x=
,
则OG=
;
(2)∵设F(x,2),则E(4,
x),
∴S四边形OCFE=8-
(2-
x)(4-x)-
×2x
=-
x2+x+4
=-
(x-2)2+5.
∴F(2,2)时,四边形OCFE的面积最大,最大值为5.
∴D(2,1),
把D(2,1)代入y=
| k |
| x |
| k |
| 2 |
∴反比例函数解析式为y=
| 2 |
| x |
把E(4,n)代入反比例解析式得:n=
| 2 |
| 4 |
| 1 |
| 2 |
②由F(1,2),得到CF=1,
由折叠得:△OGH≌△FGH,
∴OG=FG,
∵OC=AB=2,
设OG=FG=x,得到CG=2-x,
在Rt△CFG中,由勾股定理得:FG2=CG2+CF2,即x2=(2-x)2+1,
整理得:4x=5,
解得:x=
| 5 |
| 4 |
则OG=
| 5 |
| 4 |
(2)∵设F(x,2),则E(4,
| 1 |
| 2 |
∴S四边形OCFE=8-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 4 |
=-
| 1 |
| 4 |
∴F(2,2)时,四边形OCFE的面积最大,最大值为5.
看了 如图,矩形OABC的顶点A,...的网友还看了以下:
若a是第四象限角,求a/3所在象限,并将a/3的范围在坐标系中表示已知角α是第四象限的角,求α/3 2020-04-05 …
锐角是第几象限角?第一象限角一定是锐角吗?再分别就直角 钝角来回答这两个问题. 2020-04-06 …
如图,M是四边形ABCD对角线的交点,AC⊥x轴于点C,BD⊥y轴于点B.反比例函数C1:y=4x 2020-04-08 …
已知角2α的终边在x轴的上方,那么α是()A.第一象限角B.第一、二象限角C.第一、三象限角D.第 2020-05-14 …
已知反比例函数y=k/x的图象经A(-根号3,m)过点A作AB垂直于X轴于点B且三角形的面积为根号 2020-05-15 …
锐角是第几象限的角?第一象限角一定是锐角吗?直角在第几象限?钝角在第几象限?我在此先谢过了! 2020-05-16 …
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)B(-4,0)(1)求经过点C的 2020-05-17 …
教室中各个角落的同学都能看见黑板上的字,是因为此时黑板发生反射的结果,黑板用久了后出现“反光”现象 2020-05-17 …
三角函数下列说法正确的是哪个?终边相同的角都相等钝角是第二象限角第一象限的角是锐角第四象限的角是负 2020-05-22 …
三角恒等变换口诀解释1加余弦想余弦,1减余弦想正弦,幂升一次角减半,升幂降次它为范,三角函数反函数 2020-06-06 …