早教吧作业答案频道 -->数学-->
如图,四边形ABCD内接于O,对角线AC、BD相交于点E,且AB=AC,BD平分∠ABC,AD、BC延长线交于点F.(1)求证:∠ADB=∠CDF;(2)求证:AB=CF.
题目详情
如图,四边形ABCD内接于 O,对角线AC、BD相交于点E,且AB=AC,BD平分∠ABC,AD、BC延长线交于点F.
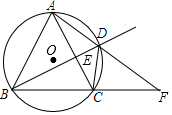
(1)求证:∠ADB=∠CDF;
(2)求证:AB=CF.

(1)求证:∠ADB=∠CDF;
(2)求证:AB=CF.
▼优质解答
答案和解析
(1)证明:∵AB=AC,
∴∠ABC=∠ACB.
∵∠ADB与∠ACB是同弧所对的圆周角,
∴∠ADB=∠ACB.
∵∠CDF=∠ABC,
∴∠ADB=∠CDF;
(2)证明:∵BD平分∠ABC
∴∠ABD=∠CBD.
∵∠CBD=∠CAD,
∴∠ABD=∠CAD.
∵四边形ABCD是圆内接四边形,
∴∠DCF=∠BAD.
∵由(1)可知∠ADB=∠CDF,
∴∠F=∠ABD,
∴∠F=∠CAD,
∴AC=CF.
∵AB=AC,
∴AB=CF.
∴∠ABC=∠ACB.
∵∠ADB与∠ACB是同弧所对的圆周角,
∴∠ADB=∠ACB.
∵∠CDF=∠ABC,
∴∠ADB=∠CDF;
(2)证明:∵BD平分∠ABC
∴∠ABD=∠CBD.
∵∠CBD=∠CAD,
∴∠ABD=∠CAD.
∵四边形ABCD是圆内接四边形,
∴∠DCF=∠BAD.
∵由(1)可知∠ADB=∠CDF,
∴∠F=∠ABD,
∴∠F=∠CAD,
∴AC=CF.
∵AB=AC,
∴AB=CF.
看了 如图,四边形ABCD内接于O...的网友还看了以下:
(1)把原图按2:1的比放大,放大后的图形A点的对应位置是(3,10);(2)把原图绕A点顺时针旋 2020-04-06 …
如图,已知在平行四边形ABCD中,E为AD的中点,CE的延长线交BA的延长于点F.(1)求证:CD 2020-05-13 …
如图,在正方形ABCD中,AB=4a,E是AB的中点,DF=3AF (1)求EF的长 (2)求证: 2020-05-15 …
物理并联电路图 题将一段粗细均匀的电阻丝围成正方形 测得AB间的电阻为15欧 其中B点为该边的中点 2020-05-16 …
如图,四边形ABCD是梯形,点E是上底边AD上一点,CE的延长线与BA的延长线交于点F,过点E作B 2020-06-23 …
草场上有个木屋,木屋是边长3m的正方形,A点是木屋一角,在A点处有一根木桩,用6m长的绳子栓一匹马 2020-06-29 …
(2000•海淀区)已知:如图,四边形ABCD是⊙O的内接四边形,A是弧BD的中点,过A点的切线与 2020-07-20 …
在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点 2020-07-30 …
如图,四边形ABCD是梯形,点E是上底边AD上一点,CE的延长线与BA的延长线交于点F,过点E作B 2020-08-01 …
如图,已知四边形ABCD中,AB平行CD,以AD、AC为边做平行四边形ACED,延长DC交EB于F 2020-08-03 …