早教吧作业答案频道 -->数学-->
如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D(Ⅰ)证明:BD=DF;(Ⅱ)若∠D=∠EBC,求证:AB2BD2=AFCD.
题目详情
如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D
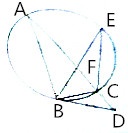
(Ⅰ)证明:BD=DF;
(Ⅱ)若∠D=∠EBC,求证:
=
.

(Ⅰ)证明:BD=DF;
(Ⅱ)若∠D=∠EBC,求证:
| AB2 |
| BD2 |
| AF |
| CD |
▼优质解答
答案和解析
证明:(Ⅰ)∵过点B作圆的切线交AC的延长线于点D,
∴∠CBD=∠A,
∵∠ABC的平分线BF交圆于点E,
∴∠ABF=∠CBF,
∵∠CFB=∠A+∠ABF,
∴∠CFB=∠DBF,
∴BD=DF;
(Ⅱ)∵BD是切线,
∴∠DBC=∠A,
又∵∠BDC=∠ADB,
∴△BDC∽△ADB,
∴
=
=
,
∴BD2=AD×DC,
=
∵∠D=∠EBC,∠CFB=∠DBF,∠ACB=∠CBD+∠D
∴△DBF∽△BCF,
∴
=
,
∵
=
,
∴
=
,
∵BF=BC,
∴
=
,
∵∠ABC的平分线BF交圆于点E,
∴利用角平分线的性质可得
=
,
∴
=
,
∴
=
,
∴AB2=AD×AF,
∵BD2=AD×DC,
∴
=
.
∴∠CBD=∠A,
∵∠ABC的平分线BF交圆于点E,
∴∠ABF=∠CBF,
∵∠CFB=∠A+∠ABF,
∴∠CFB=∠DBF,
∴BD=DF;
(Ⅱ)∵BD是切线,
∴∠DBC=∠A,
又∵∠BDC=∠ADB,
∴△BDC∽△ADB,
∴
| BD |
| AD |
| DC |
| DB |
| BC |
| AB |
∴BD2=AD×DC,
| BD |
| BC |
| AD |
| AB |
∵∠D=∠EBC,∠CFB=∠DBF,∠ACB=∠CBD+∠D
∴△DBF∽△BCF,
∴
| DB |
| BC |
| BF |
| CF |
∵
| BD |
| BC |
| AD |
| AB |
∴
| BF |
| CF |
| AD |
| AB |
∵BF=BC,
∴
| BC |
| CF |
| AD |
| AB |
∵∠ABC的平分线BF交圆于点E,
∴利用角平分线的性质可得
| AB |
| BC |
| AF |
| CF |
∴
| BC |
| CF |
| AB |
| AF |
∴
| AB |
| AF |
| AD |
| AB |
∴AB2=AD×AF,
∵BD2=AD×DC,
∴
| AB2 |
| BD2 |
| AF |
| CD |
看了 如图,△ABC为圆的内接三角...的网友还看了以下:
已知f(x)在R上是增函数,对任意实数x,都有f(x)0试比较f(a)+f(b)与f(-a)+f( 2020-05-13 …
在平面直角坐标系中,已知焦距为4的椭圆C:x^2/a^2+y^2/b^2=1(a>b>0)的右焦点 2020-05-15 …
已知a,b属于N*,f(a+b)=f(a)·f(b),f(1)=2则f(2)∕f(1)+f(3)∕ 2020-06-03 …
在等边△ABC中,AB=2,点P为AB边上任一点,过点P作PE垂直BC于E,过E作EF垂直AC于F 2020-07-30 …
一个导数问题的理解设f(x)在[a,b]上连续,在(a,b)内可导且不恒于常数,f(a)=f(b) 2020-07-31 …
证明原函数和反函数单调性相同已知y=f(x)在[a,b]上是增函数,求证y=f-1(x)在[f(a 2020-08-01 …
f(a)+f(b)=2f[(a+b)/2]*f[(a-b)/2]的奇偶性已知函数f(x)对于任意实 2020-08-01 …
椭圆x^2/a^2+y^2/b^2=1(a>b>0)的右焦点为F,离心率是1/2,过F作直线l交椭 2020-08-01 …
(本小题满分14分)已知椭圆的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作,其中 2020-08-01 …
两道高一数学题1.一束光线过点P(2,3)射到直线X+Y+1=0后,反射后经过点(1,1)点,求入射 2020-12-07 …