我国魏晋时期的数学家刘徽创立了“割圆术”，认为圆内接正多边形边数无限增加时，周长就越接近圆周长，由此求得了圆周率π的近似值，设半径为r的圆内接正n边形的周长为L，圆的直径

Question

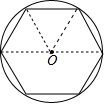
我国魏晋时期的数学家刘徽创立了“割圆术”，认为圆内接正多边形边数无限增加时，周长就越接近圆周长，由此求得了圆周率π的近似值，设半径为r的圆内接正n边形的周长为L，圆的直径为d，如图所示，当n=6时，π≈ (L)/(d)= (6r)/(2r)=3，那么当n=12时，π≈ (L)/(d)=___．（结果精确到0.01，参考数据：sin15°=cos75°≈0.259）

Answer 1

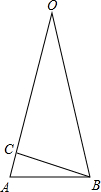如图，圆的内接正十二边形被半径分成如图所示的十二个等腰三角形，其顶角为30°，即∠O=30°，∠ABO=∠A=75°，
作BC⊥AO于点C，则∠ABC=15°，
∵AO=BO=r，
∴BC=(1)/(2)r，OC=(1)/(2)√(3)r，
∴AC=（1-(1)/(2)√(3)）r，
∵Rt△ABC中，cosA=(AC)/(AB)，
即0.259=((1-(1)/(2)√(3))r)/(AB)，
∴AB≈0.517r，
∴L=12×0.517r=6.207r，
又∵d=2r，
∴π≈(L)/(d)=(6.207r)/(2r)≈3.10，
故答案为：3.10