早教吧作业答案频道 -->数学-->
如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ=.
题目详情
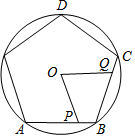
如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ=___.

▼优质解答
答案和解析
连接OA、OB、OC,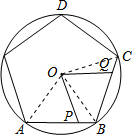
∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,
,
∴△OBP≌△OCQ,
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故答案为:72°.

∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,
|
∴△OBP≌△OCQ,
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故答案为:72°.
看了 如图,P、Q分别是⊙O的内接...的网友还看了以下:
如图,在△ABC中,AB=4cm,BC=8cm,点P从点A开始沿AB边向B以1cm/s的速度移动, 2020-05-16 …
(1)P:a>b,Q:a>b-1,P是Q的什么条件我做出来P是Q的充分条件,感觉不太对(2)P:a 2020-06-02 …
正余弦综合应用1.在三角形ABC中,a,b,c分别为三个内角A,B,C所对的边,两个向量P=(a+ 2020-06-03 …
把下列各式化成(a-b)^p的形式Ⅰ15(a-b)³[-6(a-b)^(q+5)](b-a)²是不 2020-07-18 …
C中求三角形面积问题#include#includevoidmain(){doublea,b,c, 2020-07-23 …
C语言求三角形面积问题#include#includevoidmain(){doublea,b,c 2020-07-23 …
等边三角形ABC中,P为BC边上一点,设以AP、BP、CP为边组成的新三角形的最大内角为Q,则Q( 2020-07-24 …
由下列命题构成的“p或q”,“p且q”形式的复合命题均为真命题的是()A.p:a∈{a,b,c}, 2020-08-01 …
日本人酷爱樱花,把它称之为“国花”,在樱花盛开的季节,人们常在樱花树下野餐聚会,结合下图,回答9-1 2020-11-13 …
日本有“樱花之国”称号,右图是日本气象株式会社发布的樱花开放时间预测,读图回答5~7题.导致日本樱花 2021-01-13 …