如图，一个半径为r的圆形纸片在边长为a（a≥23r）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（）A.π3r2B.(33-π)3r2C.(33-π)r2D.πr2

Question

如图，一个半径为r的圆形纸片在边长为a（a≥2

√(3)r）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（　　）

A.

(π)/(3)r2

B.

((3√(3)-π))/(3)r2

C. (3

√(3)-π)r2

D. πr²

Answer 1

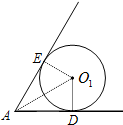如图，当圆形纸片运动到与∠A的两边相切的位置时，
过圆形纸片的圆心O₁作两边的垂线，垂足分别为D，E，
连AO₁，则Rt△ADO₁中，∠O₁AD=30°，O₁D=r，AD=√(3)r．
∴S△ADO1=(1)/(2)O1D•AD=(√(3))/(2)r2．由S四边形ADO1E=2S△ADO1=√(3)r2．
∵由题意，∠DO₁E=120°，得S扇形O1DE=(π)/(3)r2，
∴圆形纸片不能接触到的部分的面积为3(√(3)r2-(π)/(3)r2)=(3√(3)-π)r2．
故选：C．