早教吧作业答案频道 -->数学-->
四边形ABCD中,E是BC的中点,BC=4,且∠AED=∠B=∠C=60°.(1)如图1,若AD∥BC,求证:△ADE是等边三角形;(2)如图2,若AD不平行于BC,过点E作EM⊥AD于M,求EM的长.
题目详情
四边形ABCD中,E是BC的中点,BC=4,且∠AED=∠B=∠C=60°.
(1)如图1,若AD∥BC,求证:△ADE是等边三角形;
(2)如图2,若AD不平行于BC,过点E作EM⊥AD于M,求EM的长.
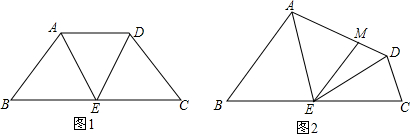
(1)如图1,若AD∥BC,求证:△ADE是等边三角形;
(2)如图2,若AD不平行于BC,过点E作EM⊥AD于M,求EM的长.

▼优质解答
答案和解析
 (1)证明:∵AD∥BC,∠B=∠C=60°,
(1)证明:∵AD∥BC,∠B=∠C=60°,
∴AB=CD,
∵E是BC的中点,
∴BE=CE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE,
∴AE=DE,
又∵∠AED=60°,
∴△ADE是等边三角形;
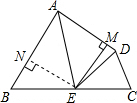
(2) 过点E作EN⊥AB于点N,
∵∠AED=60°,
∴∠AEB+∠DEC=120°,
∵∠B=60°,
∴∠BAE+∠AEB=120°,
∴∠BAE=∠DEC,
又∵∠B=∠C=60°,
∴△ABE∽△ECD,
∴
=
,
∴AB•ED=EC•EA,
∵E是BC的中点,
∴EB=EC,
∴AB•DE=BE•AE,
∴
=
,
又∵∠AED=∠B=60°,
∴△ABE∽AED,
∴∠BAE=∠DAE,
∵NE⊥AB,EM⊥AD,
∴NE=EM,
∴sin60°=
,
∵BE=EC,
∴
=
=
,
∵BC=4,
∴EM=
.
 (1)证明:∵AD∥BC,∠B=∠C=60°,
(1)证明:∵AD∥BC,∠B=∠C=60°,∴AB=CD,
∵E是BC的中点,
∴BE=CE,
在△ABE和△DCE中,
|
∴△ABE≌△DCE,
∴AE=DE,
又∵∠AED=60°,
∴△ADE是等边三角形;
(2) 过点E作EN⊥AB于点N,
∵∠AED=60°,
∴∠AEB+∠DEC=120°,
∵∠B=60°,
∴∠BAE+∠AEB=120°,
∴∠BAE=∠DEC,
又∵∠B=∠C=60°,
∴△ABE∽△ECD,
∴
| AB |
| EC |
| AE |
| DE |
∴AB•ED=EC•EA,
∵E是BC的中点,
∴EB=EC,
∴AB•DE=BE•AE,
∴
| AB |
| BE |
| AE |
| DE |
又∵∠AED=∠B=60°,
∴△ABE∽AED,
∴∠BAE=∠DAE,
∵NE⊥AB,EM⊥AD,
∴NE=EM,
∴sin60°=
| NE |
| BE |
| ||
| 2 |
∵BE=EC,
∴
| EN |
| BC |
| EM |
| BC |
| ||
| 4 |
∵BC=4,
∴EM=
| 3 |
看了 四边形ABCD中,E是BC的...的网友还看了以下:
读图,A、B、D、E三点在晨昏线上,据此完成问题。小题1:下列叙述正确的是A.下一刻D点将进入白昼 2020-06-12 …
圆的计算题回答者+30分哦圆:r半径d直径c周长s面积r=12s=d=2.4c=c=62.8d=r 2020-07-18 …
(18分)如图所示,定滑轮B、C与动滑轮D组成一滑轮组,各滑轮与转轴间的摩擦、滑轮的质量均不计.在 2020-07-31 …
读《美国部分地区轮廓图》,据此回答下题:(1)图中a、b、c、d、e区域中,属于商品谷物农业地域类型 2020-11-05 …
下图反映四个国家的人口出生率和死亡率。据此回答1-2题:1.其中人口自然增长率最高的国家是:()A. 2020-11-11 …
读江南丘陵某地区等高线地形图,回答下列各题。1.当该地区普降暴雨时,水位上涨最猛的是A.①河B.②河 2020-11-23 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
如图,由图1的三角形ABC沿DE折叠得到图2,图3,图4.(1)如图2,猜想角BDA+角CEA与角A 2020-12-25 …
读图7-5,完成1、2题。1图中全部属于温带季风气候的岛屿或半岛是()A.④B.③C.②D.①2图中 2020-12-28 …
下列绘画作品中,最能体现中国古代文人风貌的是图1图2图3图4[]A.《天工开物》插图B、《清明上河图 2021-01-15 …