早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.(1)求点E的
题目详情
在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.
(1)求点E的坐标;
(2)△AEC能否为直角三角形?若能,求出此时抛物线的函数表达式;若不能,请说明理由.

(1)求点E的坐标;
(2)△AEC能否为直角三角形?若能,求出此时抛物线的函数表达式;若不能,请说明理由.
▼优质解答
答案和解析
(1)如图所示:设此抛物线对称轴与x轴交于点F,
∴S△DEC:S△AEC=DO:AF=3:4,
∵DO∥AF,
∴△EDO∽△EAF,
∴EO:EF=DO:AF=3:4,
∴EO:OF=3:1,
由y=mx2-2mx+n(m<0)得:A(1,n-m),D(0,n),
∴OF=1,
∴EO=3,
∴E(-3,0);
(2)∵DO:AF=3:4,
∴
=
,
∴n=-3m,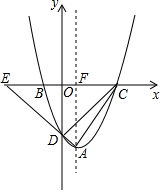
∴y=mx2-2mx-3m=m(x2-2x-3)
=m(x-3)(x+1),
∴B(-1,0),C(3,0),A(1,-4m),
由题意可知,AE,AC不可能与x轴垂直,
∴若△AEC为直角三角形,则∠EAC=90°,
又∵AF⊥EC,可得△EFA∽△AFC,
∴
=
,即
=
,
∵m<0,
∴m=-
,
∴二次函数解析式为:y=-
x2+
x+
.
∴S△DEC:S△AEC=DO:AF=3:4,
∵DO∥AF,
∴△EDO∽△EAF,
∴EO:EF=DO:AF=3:4,
∴EO:OF=3:1,
由y=mx2-2mx+n(m<0)得:A(1,n-m),D(0,n),
∴OF=1,
∴EO=3,
∴E(-3,0);
(2)∵DO:AF=3:4,
∴
| n |
| n-m |
| 3 |
| 4 |
∴n=-3m,

∴y=mx2-2mx-3m=m(x2-2x-3)
=m(x-3)(x+1),
∴B(-1,0),C(3,0),A(1,-4m),
由题意可知,AE,AC不可能与x轴垂直,
∴若△AEC为直角三角形,则∠EAC=90°,
又∵AF⊥EC,可得△EFA∽△AFC,
∴
| EF |
| AF |
| AF |
| CF |
| 4 |
| -4m |
| -4m |
| 2 |
∵m<0,
∴m=-
| ||
| 2 |
∴二次函数解析式为:y=-
| ||
| 2 |
| 2 |
3
| ||
| 2 |
看了 在平面直角坐标系xOy中,抛...的网友还看了以下:
抛物线y=ax^2+bx+c交x轴于A、B两点,与y轴交于点C,已知抛物线的对称轴为x=1,B(3 2020-05-15 …
有X,Y,Z三种元素,X和Y可形成XY和XY2两种化合物;Z与X,Y分别形成XZ4和Z2Y两种化合 2020-05-16 …
有相对原子质量均大于10的A、B两种元素,有相对原子质量均大于10的两种元素,它们可以形成化合物X 2020-05-16 …
X和Z是由A、B、C三种元素(A、B、C均为1~18号元素)形成的两种化合物.已知元素A在两种化合 2020-06-05 …
A是一种常见化合物,在通电条件下分解为B、C两种气态单质.其中B与某黑色氧化物X在加热条件下玍成一 2020-06-05 …
下列情形时,如果a>0,抛物线y=a*x^2+b*x+c的顶点在顶点在什么?(1)方程a*x^2+ 2020-07-29 …
关于绝对值的不等式和集合的题1.已知集合A={1,2},B={x|x是A的子集},则集合B=?2. 2020-08-03 …
大学物理——求绳的张力质量m=2kg的匀质细绳,长为L=1m,两端分别连接重物A和B,Ma=8kg, 2020-11-01 …
A中加入X生成B,B中加入X生成C.请分别推断ABC是什么物质(两题)1若ABCA的焰色反应均为黄色 2020-11-03 …
抛物线y=ax2+bx+c交x轴于A、B两点,交y于点C,已知抛物线的对称轴为x=1B(3,0),C 2020-11-27 …