早教吧作业答案频道 -->数学-->
已知等腰直角△ABC中,∠BAC=90°,AB=AC=2,动点P在直线BC上运动(不与点B、C重合).(1)如图1,点P在线段BC上,作∠APQ=45°,PQ交AC于点Q.①求证:△ABP∽△PCQ;②当△APQ是等腰三角形时,
题目详情
已知等腰直角△ABC中,∠BAC=90°,AB=AC=2,动点P在直线BC上运动(不与点B、C重合).
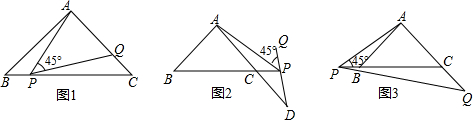
(1)如图1,点P在线段BC上,作∠APQ=45°,PQ交AC于点Q.
①求证:△ABP∽△PCQ;②当△APQ是等腰三角形时,求AQ的长.
(2)①如图2,点P在BC的延长线上,作∠APQ=45°,PQ的反向延长线与AC的延长线相交于点D,是否存在点P,使△APD是等腰三角形?若存在,写出点P的位置;若不存在,请简要说明理由;
②如图3,点P在CB的延长线上,作∠APQ=45°,PQ的延长线与AC的延长线相交于点Q,是否存在点P,使△APQ是等腰三角形?若存在,写出点P的位置;若不存在,请简要说明理由.
(1)如图1,点P在线段BC上,作∠APQ=45°,PQ交AC于点Q.
①求证:△ABP∽△PCQ;②当△APQ是等腰三角形时,求AQ的长.
(2)①如图2,点P在BC的延长线上,作∠APQ=45°,PQ的反向延长线与AC的延长线相交于点D,是否存在点P,使△APD是等腰三角形?若存在,写出点P的位置;若不存在,请简要说明理由;
②如图3,点P在CB的延长线上,作∠APQ=45°,PQ的延长线与AC的延长线相交于点Q,是否存在点P,使△APQ是等腰三角形?若存在,写出点P的位置;若不存在,请简要说明理由.

▼优质解答
答案和解析
(1)①∵∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°,
∵∠BAP+∠APB=135°,
∠APB+∠QPC=135°,
∴∠BAP=∠QPC,
∴△ABP∽△PCQ;
②当AP=AQ时,∠APQ=∠AQP=45°,
∴∠PAQ=90°,
∴点P与点B、点Q与点C重合,不合题意;
当AP=PQ时,∵△ABP∽△PCQ,
∴△ABP≌△PCQ,
∴AB=PC=2,
∴BP=CQ=2
-2,
∴AQ=AC-CQ=4-2
;
当AQ=PQ时,∠PAQ=∠APQ=45°,
∴∠APC=∠AQP=90°,
∴AQ=PQ=QC=1;
(2)存在,
∵∠ACB=90°,
∴∠CAP+∠APC=45°,
∵∠APQ=45°,
∴∠CAP+∠D=45°,
∴∠APC=∠D,
∴△CAP∽△PAD,
∴
=
,又AP=PD,
∴PC=AC=2;
(3)不存在,
∵P和B不重合,
∴∠PAQ>90°,
∴∠APQ=45°,∠AQP<45°,
∴AP≠AQ.
∴∠B=∠C=45°,
∵∠BAP+∠APB=135°,
∠APB+∠QPC=135°,
∴∠BAP=∠QPC,
∴△ABP∽△PCQ;
②当AP=AQ时,∠APQ=∠AQP=45°,
∴∠PAQ=90°,
∴点P与点B、点Q与点C重合,不合题意;
当AP=PQ时,∵△ABP∽△PCQ,
∴△ABP≌△PCQ,
∴AB=PC=2,
∴BP=CQ=2
| 2 |
∴AQ=AC-CQ=4-2
| 2 |
当AQ=PQ时,∠PAQ=∠APQ=45°,
∴∠APC=∠AQP=90°,
∴AQ=PQ=QC=1;
(2)存在,
∵∠ACB=90°,
∴∠CAP+∠APC=45°,
∵∠APQ=45°,
∴∠CAP+∠D=45°,
∴∠APC=∠D,
∴△CAP∽△PAD,
∴
| AC |
| AP |
| PC |
| PD |
∴PC=AC=2;
(3)不存在,
∵P和B不重合,
∴∠PAQ>90°,
∴∠APQ=45°,∠AQP<45°,
∴AP≠AQ.
看了 已知等腰直角△ABC中,∠B...的网友还看了以下:
已知椭圆C:(a>b>0)的长轴长为4,焦距为2.(I)求椭圆C的方程;(Ⅱ)过动点M(0,m)( 2020-05-15 …
已知M,P是两个不等的非空集合,则必有() A.空集属于M交P B.空集等于M交P,C.空集包含于 2020-05-16 …
如图1,抛物线y=-x2+2bx+c(b>0)与y轴交于点C,点P为抛物线顶点,分别作点P,C关于 2020-06-12 …
已知P(A)=1/2,P(B)=1/3,P(C)=1/5,P(AB)=1/10,P(AC)=1/1 2020-06-22 …
证明p(ab)+p(ac)+p(bc)≥p(a)+p(b)+p(c)-1前人栽树,后人乘凉,找不到 2020-06-29 …
在平面直角坐标系xOy中,已知椭圆C:x23+y2=1.如图所示,斜率为k(k>0)且不过原点的直 2020-07-25 …
已知抛物线C:y2=2px(p>0)的焦点为F,点P在C上且其横坐标为1,以F为圆心,|FP|为半 2020-07-31 …
已知玉米胚乳有色至少受3对基因控制,一是基本色泽基因C/c,一是紫色基因P/p,P表现紫色,p表现红 2020-11-24 …
已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动 2021-01-12 …
关于化学平衡常数和浓度积的问题化学平衡常数:c^p(C)*c^q(D)/C^m(A)*c^n(B)浓 2021-01-22 …