早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,当其中一个点到达
题目详情
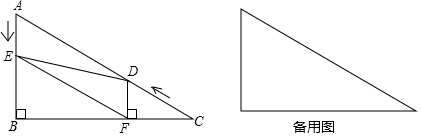
如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)当四边形BFDE是矩形时,求t的值;
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(1)求证:AE=DF;
(2)当四边形BFDE是矩形时,求t的值;
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

▼优质解答
答案和解析
(1)证明:在Rt△CDF中,∠C=30°
∴DF=
CD,
∴DF=
•4t=2,
又∵AE=2t,
∴AE=DF.
(2)当四边形BFDE是矩形时,有BE=DF,
∵Rt△ABC中,∠C=30°
∴AB=
AC=
×48=24,
∴BE=AB-AE=24-2t,
∴24-2t=2t,
∴t=6.
(3)∵∠B=90°,DF⊥BC
∴AE∥DF,∵AE=DF,
∴四边形AEFD是平行四边形,
由(1)知:四边形AEFD是平行四边形
则当AE=AD时,四边形AEFD是菱形
∴2t=48-4t,
解得t=8,又∵t≤
=
=12,
∴t=8适合题意,
故当t=8s时,四边形AEFD是菱形.
∴DF=
| 1 |
| 2 |
∴DF=
| 1 |
| 2 |
又∵AE=2t,
∴AE=DF.
(2)当四边形BFDE是矩形时,有BE=DF,
∵Rt△ABC中,∠C=30°
∴AB=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=AB-AE=24-2t,
∴24-2t=2t,
∴t=6.
(3)∵∠B=90°,DF⊥BC
∴AE∥DF,∵AE=DF,
∴四边形AEFD是平行四边形,
由(1)知:四边形AEFD是平行四边形
则当AE=AD时,四边形AEFD是菱形
∴2t=48-4t,
解得t=8,又∵t≤
| AB |
| v |
| 24 |
| 2 |
∴t=8适合题意,
故当t=8s时,四边形AEFD是菱形.
看了 如图,在Rt△ABC中,∠B...的网友还看了以下:
如图,点O是线段AB上一点,C,D两点分别从O,B同时出发,以每秒2厘米,每秒4厘米的速度在直线A 2020-06-02 …
如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐 2020-06-14 …
甲乙两人同时从AB两地出发,相向而行,甲每分钟行80米,乙每分钟行60米,两人在途中C点相遇.如果 2020-06-20 …
如图 数轴上标出若个点,每相距1个单位长度,点A,B,C,D分别对应整数a,b,c,d,且d-2= 2020-06-27 …
如图,数轴上标出若干个点,每相邻的两个点相距一个长度单位,点A B C D对应的整数a b c d 2020-06-27 …
数轴上标出若干个点,每相邻两点相距一个长度单位,点A,B,C,D对应的数分别是数a,b,c,d,且 2020-06-27 …
如图所示,数轴上标出若干个点,每相邻两点相距一个单位长度,点A,B,C,D对应的数分别是整数a,b 2020-07-13 …
如图,已知在等腰直角三角形ABC中,AB=AC=4,点D从点A出发,沿射线AB方向以每秒1个单位长 2020-07-21 …
如图,已知抛物线y=-12x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点 2020-07-29 …
ThemathtestisabigPity已知等边三角形ABC,边长为4点D从点A出发沿AB运动到点 2020-11-03 …