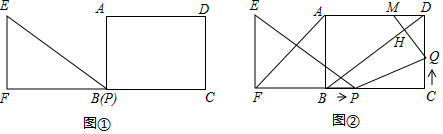
已知：Rt△EFP和矩形ABCD如图①摆放（点P与点B重合），点F，B（P），C在同一直线上，AB=EF=6cm，BC=FP=8cm，∠EFP=90°，如图②，△EFP从图①的位置出发，沿BC方向匀速运动，速度为1cm/s，EP与AB交于

Question

已知：Rt△EFP和矩形ABCD如图①摆放（点P与点B重合），点F，B（P），C在同一直线上，AB=EF=6cm，BC=FP=8cm，∠EFP=90°，如图②，△EFP从图①的位置出发，沿BC方向匀速运动，速度为1cm/s，EP与AB交于点G；同时，点Q从点C出发，沿CD方向匀速运动，速度为1cm/s．过点Q作QM⊥BD，垂足为H，交AD于点M，连接AF，FQ，当点Q停止运动时，△EFQ也停止运动．设运动时间为t（s）（0<t<6），解答下列问题：
（1）当t为何值时，PQ∥BD？
（2）设五边形AFPQM的面积为y（cm²），求y与t之间的函数关系式；
（3）在运动过程中，是否存在某一时刻t，使S_{五边形AFPQM}：S_矩形ABCD=9：8？若存在，求出t的值；若不存在，请说明理由．
（4）在运动过程中，是否存在某一时刻t，使点M在线段PG的垂直平分线上？若存在，求出t的值；若不存在，请说明理由．

Answer 1

（1）如图1中，

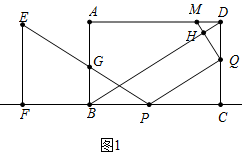
当PQ∥BD时，(CQ)/(CD)=(CP)/(CB)，
∴(t)/(6)=(8-t)/(8)，
∴t=(24)/(7)，
∴t=(24)/(7)s时，PQ∥BD．

（2）如图2中，

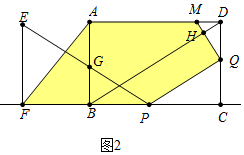
当0<t<6时，S_{五边形AFPQM}=S_梯形AFCD-S_△DMQ-S_△PQC
=(1)/(2)（8+8-t+8）•6-(1)/(2)•（6-t）•(3)/(4)（6-t）-(1)/(2)•（8-t）•t
=(1)/(8)t²-(5)/(2)t+(117)/(2)．

（3）如图2中，假设存在，则有（(1)/(8)t²-(5)/(2)t+(117)/(2)．）：48=9：8，
解得t=2或18（舍弃），
∴t=2s时，S_{五边形AFPQM}：S_矩形ABCD=9：8．

（4）存在．
理由：如图3中，连接MG、MP，作MK⊥BC于K．

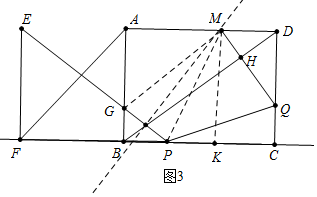
易知：AG=6-(3)/(4)t．DQ=6-t，DM=KC=(3)/(4)（6-t），PK=8-t-(3)/(4)（6-t），MK=CD=6，
∵点M在PG的垂直平分线上，
∴MG=MP，
∴AG²+AM²=PK²+MK²，
∴（6-(3)/(4)t）²+[8-(3)/(4)（6-t）]²=6²+[8-t-(3)/(4)（6-t）]²，
解得t=(32)/(17)或0（舍弃），
∴t=(32)/(17)s时，点M在线段PG的垂直平分线上