早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)当PC=CE时,求∠CDP的度数;(2)试用等式表示线段PB、BC、CE之间的数量关系,并证明.
题目详情
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
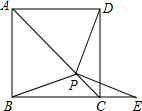
(1)当PC=CE时,求∠CDP的度数;
(2)试用等式表示线段PB、BC、CE之间的数量关系,并证明.

(1)当PC=CE时,求∠CDP的度数;
(2)试用等式表示线段PB、BC、CE之间的数量关系,并证明.
▼优质解答
答案和解析
(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BCP=∠DCP=45°,∠BCD=∠DCE=90°,
∴∠PCE=45°+90°=135°,
在△BCP和△DCP中,
,
∴△BCP≌△DCP(SAS),
∴BP=DP,∠CBP=∠CDP,
∵PE=PB,PC=CE,
∴PD=PE,∠CBP=∠PEB=∠CPE=
(180°-135°)=22.5°,
∴∠CDP=22.5°;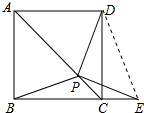
(2)BC2+CE2=2PB2,理由如下:
连接DE,如图所示:
由(1)得:∠CBP=∠CDP,PD=PE,
∵PB=PE,
∴∠CBP=∠PEB,
∴∠CDP=∠PEB,
∴P、C、E、D四点共圆,
∴∠DPE=∠DCE=90°,
由勾股定理得:DE2=CD2+CE2,DE2=PD2+PE2,
∵BC=CD,PB=PD=PE,
∴BC2+CE2=2PB2.
∴AB=BC=CD=AD,∠BCP=∠DCP=45°,∠BCD=∠DCE=90°,
∴∠PCE=45°+90°=135°,
在△BCP和△DCP中,
|
∴△BCP≌△DCP(SAS),
∴BP=DP,∠CBP=∠CDP,
∵PE=PB,PC=CE,
∴PD=PE,∠CBP=∠PEB=∠CPE=
| 1 |
| 2 |
∴∠CDP=22.5°;

(2)BC2+CE2=2PB2,理由如下:
连接DE,如图所示:
由(1)得:∠CBP=∠CDP,PD=PE,
∵PB=PE,
∴∠CBP=∠PEB,
∴∠CDP=∠PEB,
∴P、C、E、D四点共圆,
∴∠DPE=∠DCE=90°,
由勾股定理得:DE2=CD2+CE2,DE2=PD2+PE2,
∵BC=CD,PB=PD=PE,
∴BC2+CE2=2PB2.
看了 如图,在正方形ABCD中,P...的网友还看了以下:
甲、乙、丙为短周期元素形成的常见单质,A、B、C、D、E、F、G、X均为常见的化合物.B、X的式量 2020-04-08 …
如图所示,在一电场强度为E的匀强电场中放一金属空心导体,图中a、b分别为金属导体内部与空腔中的点, 2020-05-13 …
已知f(x)是定义在[-e,e]上的奇函数,当x€(0.e](€是属于符号)时,f(x)=e^x+ 2020-05-13 …
e^jn的累加怎么计算比如e^(0)+e^(-j)+e^(-2j)+e^(-3j)+e^(-4j) 2020-05-14 …
按要求填空.(1)E的一种核素的质量数为63,中子数为34.E的基态原子的核外电子排布式是基态E2 2020-05-14 …
把函数y=e^x的图像按向量a=(2,3)平移,得到y=f(x)的图像,则f(x)=?A.e^(x 2020-05-16 …
将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图①);再沿过点E 2020-05-17 …
利用Excel的图表功能,可以做出( )等统计图形。A.饼图 B.柱型图C.透视图 D.折线图E.地 2020-05-21 …
数学题..急急已知数列{an}的前n项和为Sn.对一切正整数n,点(Sn,n)都在函数f(x)㏒2 2020-06-03 …
y=e的x次方与y=e和x=1围成平面图形的面积图像花出来是什么样子?我画出的怎么不是封闭图形? 2020-06-03 …