早教吧作业答案频道 -->数学-->
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.(Ⅰ)求证:平面EFG∥平面PAD.(Ⅱ)是否存在实数λ满足PB=λAB,使得平面PBC⊥平面PAD?若存在,求
题目详情
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.
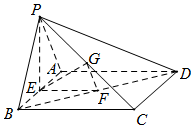
(Ⅰ)求证:平面EFG∥平面PAD.
(Ⅱ)是否存在实数λ满足PB=λAB,使得平面PBC⊥平面PAD?若存在,求出λ的值;若不存在,请说明理由.

(Ⅰ)求证:平面EFG∥平面PAD.
(Ⅱ)是否存在实数λ满足PB=λAB,使得平面PBC⊥平面PAD?若存在,求出λ的值;若不存在,请说明理由.
▼优质解答
答案和解析
(本题满分9分)
(Ⅰ)证明:连结AC.
∵底面ABCD是矩形,F是BD中点,
∴F也是AC的中点.
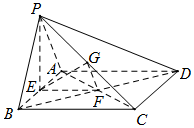
∵G是PC的中点,∴GF是△PAC的中位线,
∴GF∥PA.
∵GF⊄平面PAD,PA⊂平面PAD,
∴GF∥平面PAD.
∵E是AB中点,F是BD中点,
∴EF是△ABD的中位线,
∴EF∥AD.
∵EF⊄平面PAD,AD⊂平面PAD,
∴EF∥平面PAD.
∵GF∥平面PAD,EF∥平面PAD,EF∩FG=F,
∴平面EFG∥平面PAD. …(5分)
(Ⅱ) 存在λ,λ=
,即PB=
AB时,平面PBC⊥平面PAD.
方法一:∵PE⊥底面ABCD,BC⊂底面ABCD,AB⊂底面ABCD,
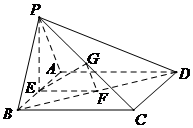 ∴PE⊥BC,PE⊥AB.
∴PE⊥BC,PE⊥AB.
∵底面ABCD是矩形,
∴AB⊥BC.
∵PE∩AB=E,
∴BC⊥平面PAB.
∵PA⊂平面PAB,
∴PA⊥BC.
∵PE⊥AB,E为AB的中点,
∴PA=PB.
当PA⊥PB,即PA=PB=
AB时,
∴PA⊥平面PBC.
∵PA⊂平面PAD,
∴平面PAD⊥平面PBC.此时 λ=
.…(9分)
方法二:过点P作PQ∥BC.
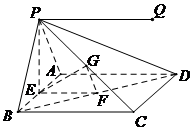
∴PQ,BC共面,即PQ⊂平面PBC.
∵底面ABCD是矩形,
∴AD∥BC.
∵PQ∥BC,
∴PQ∥AD.
∴PQ,AD共面,即PQ⊂平面PAD.
∴平面PBC∩平面PAD=PQ.
∵PE⊥底面ABCD,BC⊂底面ABCD,
∴PE⊥BC.
∵底面ABCD是矩形,
∴AB⊥BC.
∵PQ∥BC,
∴PE⊥PQ,AB⊥PQ.
∵PE∩AB=E,
∴PQ⊥平面PAB.
∵PA⊂平面PAB,PB⊂平面PAB,
∴PA⊥PQ,PB⊥PQ,
∴∠APB是平面PAD和平面PBC所成二面角的平面角.
∵平面PAD⊥平面PBC,
∴∠APB=90°.
∵PE⊥AB,E为AB的中点,
∴PA=PB.
∴△PAB是等腰直角三角形.
∴PA=
AB.即PB=
AB时,平面PBC⊥平面PAD. …(9分)
(Ⅰ)证明:连结AC.
∵底面ABCD是矩形,F是BD中点,
∴F也是AC的中点.

∵G是PC的中点,∴GF是△PAC的中位线,
∴GF∥PA.
∵GF⊄平面PAD,PA⊂平面PAD,
∴GF∥平面PAD.
∵E是AB中点,F是BD中点,
∴EF是△ABD的中位线,
∴EF∥AD.
∵EF⊄平面PAD,AD⊂平面PAD,
∴EF∥平面PAD.
∵GF∥平面PAD,EF∥平面PAD,EF∩FG=F,
∴平面EFG∥平面PAD. …(5分)
(Ⅱ) 存在λ,λ=
| ||
| 2 |
| ||
| 2 |
方法一:∵PE⊥底面ABCD,BC⊂底面ABCD,AB⊂底面ABCD,
 ∴PE⊥BC,PE⊥AB.
∴PE⊥BC,PE⊥AB.∵底面ABCD是矩形,
∴AB⊥BC.
∵PE∩AB=E,
∴BC⊥平面PAB.
∵PA⊂平面PAB,
∴PA⊥BC.
∵PE⊥AB,E为AB的中点,
∴PA=PB.
当PA⊥PB,即PA=PB=
| ||
| 2 |
∴PA⊥平面PBC.
∵PA⊂平面PAD,
∴平面PAD⊥平面PBC.此时 λ=
| ||
| 2 |
方法二:过点P作PQ∥BC.

∴PQ,BC共面,即PQ⊂平面PBC.
∵底面ABCD是矩形,
∴AD∥BC.
∵PQ∥BC,
∴PQ∥AD.
∴PQ,AD共面,即PQ⊂平面PAD.
∴平面PBC∩平面PAD=PQ.
∵PE⊥底面ABCD,BC⊂底面ABCD,
∴PE⊥BC.
∵底面ABCD是矩形,
∴AB⊥BC.
∵PQ∥BC,
∴PE⊥PQ,AB⊥PQ.
∵PE∩AB=E,
∴PQ⊥平面PAB.
∵PA⊂平面PAB,PB⊂平面PAB,
∴PA⊥PQ,PB⊥PQ,
∴∠APB是平面PAD和平面PBC所成二面角的平面角.
∵平面PAD⊥平面PBC,
∴∠APB=90°.
∵PE⊥AB,E为AB的中点,
∴PA=PB.
∴△PAB是等腰直角三角形.
∴PA=
| ||
| 2 |
| ||
| 2 |
看了 如图,在四棱锥P-ABCD中...的网友还看了以下:
建平实验学校要给操场修建塑胶跑道问所需铺设的塑胶的面积是多少平方米?建平实验学校要给操场修建塑胶跑道 2020-03-30 …
阅读材料并解决问题:我们已经知道完全平方公式可以用平面几何图形拼图来表示面积,实际上还有一些多项式 2020-05-17 …
GA=GB=100N GC=10N 斜面光滑求A受到摩擦力f和A对地面的压力FN两个截面为直角三角 2020-05-17 …
有一块正方形的实验田面积是9平方厘米,将其面积扩大喂原来的4被,则变长扩大了原来的几倍?一块正方形 2020-06-16 …
1.下列命题正确的是A;直线的平移只能形成平面B;直线饶定点直线旋转形成柱面C;直线绕定点旋转形成 2020-06-19 …
两个完全相同的梯形可以拼成一个平形四边形,平行四边形的面积等于梯形面积的(),梯两个完全相同的梯形 2020-06-27 …
(2014•扬州模拟)如图,在多面体ABCDEF中,底面ABCD是正方形,四边形BDEF是矩形,平 2020-06-27 …
下列说法正确的是:A.平面就是平行四边形B.任何一个平面图形都是一个平面C.平静的太平洋就是平面D 2020-07-31 …
平行四边形ABCD的内角C=60度,CD=2BC,沿对角线BD将平行四边形所在平面折成直二面角,求 2020-08-02 …
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底 2020-08-03 …