早教吧作业答案频道 -->数学-->
若Sn是公差不为0的等差数列{an}的前n项和,且S1,S2,S4成等比数列.(1)求等比数列S1,S2,S4的公比;(2)若S2=4,求{an}的通项公式;(3)设,Tn是数列{bn}的前n项
题目详情
若S n 是公差不为0的等差数列{a n }的前n项和,且S 1 ,S 2 ,S 4 成等比数列.
(1)求等比数列S 1 ,S 2 ,S 4 的公比;
(2)若S 2 =4,求{a n }的通项公式;
(3)设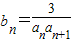 ,T n 是数列{b n }的前n项和,求使得
,T n 是数列{b n }的前n项和,求使得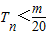 对所有n∈N * 都成立的最小正整数m.
对所有n∈N * 都成立的最小正整数m.
(1)求等比数列S 1 ,S 2 ,S 4 的公比;
(2)若S 2 =4,求{a n }的通项公式;
(3)设
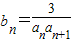 ,T n 是数列{b n }的前n项和,求使得
,T n 是数列{b n }的前n项和,求使得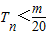 对所有n∈N * 都成立的最小正整数m.
对所有n∈N * 都成立的最小正整数m.▼优质解答
答案和解析
分析:
(1)利用数列{an}为等差数列,S1,S2,S4成等比数列.可求出首项与公差的关系,即可求得公比;(2)由S2=4,结合(1)的结论,即可求{an}的通项公式;(3)利用裂项法求数列{bn}的前n项和,确定Tn<,从而可得不等式,即可求得使得对所有n∈N*都成立的最小正整数m.
(1)∵数列{an}为等差数列,∴S1=a1,S2=2a1+d,S4=4a1+6d,∵S1,S2,S4成等比数列,∴S1?S4=S22,∴,∴∵公差d不等于0,∴d=2a1∴;(2)∵S2=4,∴2a1+d=4,又d=2a1,∴a1=1,d=2,∴an=2n-1. (3)∵∴…=要使对所有n∈N*恒成立,∴,∴m≥30,∵m∈N*,∴m的最小值为30.
点评:
本题考查等差数列与等比数列的结合,考查数列的通项与求和,考查恒成立问题,正确求和是关键.
分析:
(1)利用数列{an}为等差数列,S1,S2,S4成等比数列.可求出首项与公差的关系,即可求得公比;(2)由S2=4,结合(1)的结论,即可求{an}的通项公式;(3)利用裂项法求数列{bn}的前n项和,确定Tn<,从而可得不等式,即可求得使得对所有n∈N*都成立的最小正整数m.
(1)∵数列{an}为等差数列,∴S1=a1,S2=2a1+d,S4=4a1+6d,∵S1,S2,S4成等比数列,∴S1?S4=S22,∴,∴∵公差d不等于0,∴d=2a1∴;(2)∵S2=4,∴2a1+d=4,又d=2a1,∴a1=1,d=2,∴an=2n-1. (3)∵∴…=要使对所有n∈N*恒成立,∴,∴m≥30,∵m∈N*,∴m的最小值为30.
点评:
本题考查等差数列与等比数列的结合,考查数列的通项与求和,考查恒成立问题,正确求和是关键.
看了 若Sn是公差不为0的等差数列...的网友还看了以下:
根据4位同学对化学式“H2O”的理解:表示水这种物质;表示1个水分子由2个氢原子和1个氧原子构成; 2020-05-13 …
甲数的3分之2与乙的4分之3相等,甲数相当于乙数的(),相当于甲乙两数和的()甲数除以乙数的商是4 2020-05-14 …
解脲支原体大于等于10的4次方严重吗?CT:阴性支原体培养+鉴定+计数+药敏解脲支原体大于等于10 2020-05-17 …
(1/2)有个酒瓶在底部是个圆柱体,这部分占酒瓶3/4的高度,瓶子上面的1/4是不规则体,瓶子未满 2020-05-17 …
概率好的挑战一下:口袋里放有10个大小完全一样的球,其中3个红色的,4个白色的,3个蓝色的.口袋里 2020-05-17 …
某油田12月份原油产量是2.96x10的4次方t,当...某油田12月份原油产量是2.96x10的 2020-05-21 …
24/4=6这个算式表示的的意义(1)·把24个苹果平均分成6份,每份4个(2)把24个苹果平均分 2020-05-21 …
一捆电线,长320米,第一天用去全长的1/2,第二天用去余下的1/3,第三天用去余下的1/4··· 2020-06-05 …
尽量写的简单点我才大一,设有n个正整数(n≤20),将它们联接成一排,组成一个最大的多位整数.例如 2020-06-11 …
某数的4倍加上4,小岗错误的计算成先加上4,再乘4,结果是正确得数的3倍,这个数是几?(不可以用X 2020-06-14 …