早教吧作业答案频道 -->数学-->
问题情境如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.探究发现(1)请你判断AM、AD、MC三条线段的数量关系,并说明理由(2)AM=DE+BM是否成立?若成
题目详情
【问题情境】
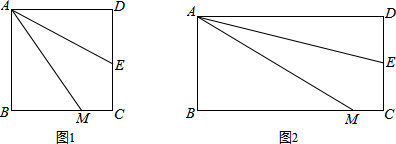
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究发现】
(1)请你判断AM、AD、MC三条线段的数量关系,并说明理由
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,上述(1)、(2)中的结论是否仍然成立?请分别作出判断,不需要证明.
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究发现】
(1)请你判断AM、AD、MC三条线段的数量关系,并说明理由
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,上述(1)、(2)中的结论是否仍然成立?请分别作出判断,不需要证明.

▼优质解答
答案和解析
证明:证明:延长AE、BC交于点N,如图1(1),
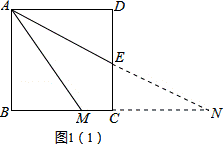
∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AD∥BC.
∴∠DAE=∠ENC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠ENC=∠MAE.
∴MA=MN.
∴△ADE≌△NCE(AAS)
∴AD=NC.
∴MA=MN=NC+MC=AD+MC.
(2)AM=DE+BM成立.
证明:如图1(2)所示.
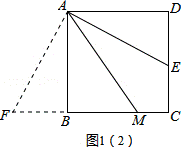
∵四边形ABCD是正方形,
∵四边形ABCD是矩形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC.
∵AF⊥AE,
∴∠FAE=90°.
∴∠FAB=90°-∠BAE=∠DAE.
∴△ABF≌△ADE(ASA).
∴BF=DE,∠F=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM.
∴∠F=∠FAM.
∴AM=FM.
∴AM=FB+BM=DE+BM.
(3)①结论AM=AD+MC仍然成立.
证明:延长AE、BC交于点P,如图2(1),
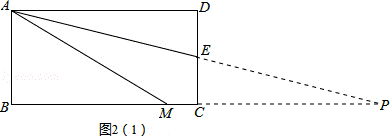
∵四边形ABCD是矩形,
∴AD∥BC.
∴∠DAE=∠EPC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠EPC=∠MAE.
∴MA=MP.
∴△ADE≌△PCE(AAS).
∴AD=PC.
∴MA=MP=PC+MC=AD+MC.
②结论AM=DE+BM不成立.
证明:假设AM=DE+BM成立.过点A作AQ⊥AE,交CB的延长线于点Q,如图2(2)所示.
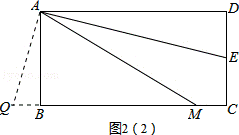
∵四边形ABCD是矩形,
∴∠BAD=∠D=∠ABC=90°,AB∥DC.
∵AQ⊥AE,
∴∠QAE=90°.
∴∠QAB=90°-∠BAE=∠DAE.
∴∠Q=90°-∠QAB=90°-∠DAE=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠QAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM
=∠BAM+∠QAB,
∴∠Q=∠QAM.
∴AM=QM.
∴AM=QB+BM.
∵AM=DE+BM,
∴QB=DE.
∴△ABQ≌△ADE(AAS),
∴AB=AD.与条件“AB≠AD“矛盾,故假设不成立.
∴AM=DE+BM不成立.

∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AD∥BC.
∴∠DAE=∠ENC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠ENC=∠MAE.
∴MA=MN.
∴△ADE≌△NCE(AAS)
∴AD=NC.
∴MA=MN=NC+MC=AD+MC.
(2)AM=DE+BM成立.
证明:如图1(2)所示.

∵四边形ABCD是正方形,
∵四边形ABCD是矩形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC.
∵AF⊥AE,
∴∠FAE=90°.
∴∠FAB=90°-∠BAE=∠DAE.
∴△ABF≌△ADE(ASA).
∴BF=DE,∠F=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM.
∴∠F=∠FAM.
∴AM=FM.
∴AM=FB+BM=DE+BM.
(3)①结论AM=AD+MC仍然成立.
证明:延长AE、BC交于点P,如图2(1),

∵四边形ABCD是矩形,
∴AD∥BC.
∴∠DAE=∠EPC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠EPC=∠MAE.
∴MA=MP.
∴△ADE≌△PCE(AAS).
∴AD=PC.
∴MA=MP=PC+MC=AD+MC.
②结论AM=DE+BM不成立.
证明:假设AM=DE+BM成立.过点A作AQ⊥AE,交CB的延长线于点Q,如图2(2)所示.

∵四边形ABCD是矩形,
∴∠BAD=∠D=∠ABC=90°,AB∥DC.
∵AQ⊥AE,
∴∠QAE=90°.
∴∠QAB=90°-∠BAE=∠DAE.
∴∠Q=90°-∠QAB=90°-∠DAE=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠QAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM
=∠BAM+∠QAB,
∴∠Q=∠QAM.
∴AM=QM.
∴AM=QB+BM.
∵AM=DE+BM,
∴QB=DE.
∴△ABQ≌△ADE(AAS),
∴AB=AD.与条件“AB≠AD“矛盾,故假设不成立.
∴AM=DE+BM不成立.
看了问题情境如图1,四边形ABCD...的网友还看了以下:
1.若x是非零自然数,y=x^4+2x^3+2x^2+2x+1,则()A.y一定是完全平方数B.y 2020-06-07 …
1.已知X=100...00(N个0)100000...00(N+1个0)50则()A.X是完全平 2020-07-16 …
完全平方数(选择题)已知数x=100…00100…0050,则}}n个0n+1个零Ax是完全平方数 2020-07-31 …
已知数x=100…00100…005,n个0,n+1个0则()A.x是完全平方数B.(x-50)是 2020-07-31 …
若实数abc满足a平方+b平方=1,b平方+c平方=2.c平方+a平方=2,则ab+bc+ac的最 2020-07-31 …
一个二次函数怎么知道它有共轭复根我记得一个二次函数有一个求解的公式,好像是2a分子负B加减根号下b 2020-08-02 …
数学勾股定理,判断对错判断对错,错误的要简述理由①△ABC中,a平方+b平方≠c平方,则△ABC不 2020-08-02 …
下列说法错误的是A-3是的平方根B平方根5等于5C-1的平方根是±1下列说法错误的是A-3是的平方 2020-08-03 …
已知x=100…0n个00100…0n+1个050,则()A.x是完全平方数B.x-25是完全平方 2020-08-03 …
1已知4a平方+4a+b平方-6b+10=0则a三次方b+ab三次方=2已知a+b=7,ab=2则 2020-08-03 …