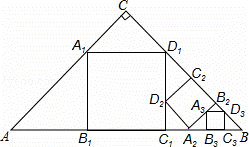
如图，△ABC，∠C=90°，AC=BC=a，在△ABC中截出一个正方形A1B1C1D1，使点A1，D1分别在AC，BC边上，边B1C1在AB边上；

Question

  如图， △ ABC ， ∠ C=90 ° ， AC=BC=a ，在 △ ABC 中截出一个正方形 A ₁ B ₁ C ₁ D ₁ ，使点 A ₁ ， D ₁ 分别在 AC ， BC 边上，边 B ₁ C ₁ 在 AB 边上；在 △ BC ₁ D ₁ 在截出第二个正方形 A ₂ B ₂ C ₂ D ₂ ，使点 A ₂ ， D ₂ 分别在 BC ₁ ， D ₁ C ₁ 边上，边 B ₂ C ₂ 在 BD ₁ 边上； … ，依此方法作下去，则第 n 个正方形的边长为 　 ．

Answer 1

（ ） ⁿ a 　

  设正方形 A ₁ B ₁ C ₁ D ₁ 的边长为 x ，

∵△ CA ₁ D ₁ 和 △ AA ₁ B ₁ 都是等腰直角三角形，

∴ A ₁ C= x ， AA ₁ = x ，

∴ x+ x=a ，解得 x= a ，

即第 1 个正方形的边长为 a ，

设正方形 A ₂ B ₂ C ₂ D ₂ 的边长为 y ，

∵△ C ₂ D ₁ D ₂ 和 △ C ₁ A ₂ D ₂ 都是等腰直角三角形，

∴ C ₁ D ₂ = y ， D ₁ D ₂ = y ，

∴ y+ y= a ，解得 y= （ ） ² a ，

即第 2 个正方形的边长为（ ） ² a ，

同理可得第 3 个正方形的边长为（ ） ³ a ，

∴ 第 n 个正方形的边长为（ ） ⁿ a ．

故答案为（ ） ⁿ a ．