早教吧作业答案频道 -->数学-->
已知函数f(x)=log3x-1x+1,g(x)=-2ax+a+1,h(x)=f(x)+g(x).(Ⅰ)当a=-1时,证明h(x)是奇函数;(Ⅱ)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
题目详情
已知函数f(x)=log3
,g(x)=-2ax+a+1,h(x)=f(x)+g(x).
(Ⅰ)当a=-1时,证明h(x)是奇函数;
(Ⅱ)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
| x-1 |
| x+1 |
(Ⅰ)当a=-1时,证明h(x)是奇函数;
(Ⅱ)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
▼优质解答
答案和解析
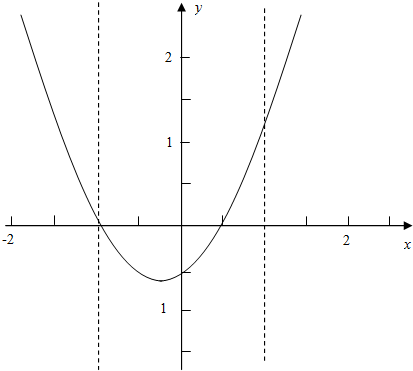 (Ⅰ)证明:当a=-1时,
(Ⅰ)证明:当a=-1时,
f(x)=log3
,g(x)=2x,
h(x)=log3
+2x,
定义域为(-∞,-1)∪(1,+∞),
又∵h(-x)=log3
-2x,
∴h(x)+h(-x)=log3
+log3
+2x-2x=0,
故h(x)为奇函数;
(Ⅱ)∵f(x)=log3g(x),
∴
=-2ax+a+1,且x∈(-∞,-1)∪(1,+∞),
∴(1-2x)a=
-1=-
,
显然a≠0,
∴
=(x+1)(x-
),
利用图象可知,当
>1时,
方程
=(x+1)(x-
)在(-∞,-1)∪(1,+∞)内有两个不等实数根,
解得0<a<1.
 (Ⅰ)证明:当a=-1时,
(Ⅰ)证明:当a=-1时,f(x)=log3
| x-1 |
| x+1 |
h(x)=log3
| x-1 |
| x+1 |
定义域为(-∞,-1)∪(1,+∞),
又∵h(-x)=log3
| x+1 |
| x-1 |
∴h(x)+h(-x)=log3
| x-1 |
| x+1 |
| x+1 |
| x-1 |
故h(x)为奇函数;
(Ⅱ)∵f(x)=log3g(x),
∴
| x-1 |
| x+1 |
∴(1-2x)a=
| x-1 |
| x+1 |
| 2 |
| x+1 |
显然a≠0,
∴
| 1 |
| a |
| 1 |
| 2 |
利用图象可知,当
| 1 |
| a |
方程
| 1 |
| a |
| 1 |
| 2 |
解得0<a<1.
看了已知函数f(x)=log3x-...的网友还看了以下:
若函数y=1/2(x^2-100x+|x^2-100x+196|),则当自变量x取1,2,3,……, 2020-03-30 …
食堂存煤15吨,可使用的天数t和平均每天的用煤量Q(千克)的函数关系为,这个函数是函数. 2020-04-25 …
若函数f(x)=a的x次方-x-a(a大于0且a不等于1)有两个零点,则实数a的取值范围是?我知道 2020-05-13 …
关于反函数的一个问题函数y=log2((1+x)/(1-x))的反函数为什么不是y=2^((1+x 2020-05-21 …
反比例函数是函数的一种特殊情况吗? 2020-05-22 …
PGP是一种电子邮件安全方案,它一般采用的散列函数是( )。A) DSS B) RSA C) DES 2020-05-23 …
PGP是一种电子邮件安全方案,它一般采用的散列函数是( )。A)DSSB)RSAC)DES D)SH 2020-05-23 …
设逻辑函数则与f等价的逻辑函数是( )。A.a+cB.a+bC.D. 2020-05-23 …
PGP是一种电子邮件安全方案,它一般采用的散列函数是()。A.DSSB.RSAC.DESD.SHA 2020-05-24 …
操作系统必须提供一种启动进程的机制。在Windows和OS/2中启动进程的函数是()。A.EXEC函 2020-05-24 …