如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，且OB=OC，下列结论：①b>1且b≠2；②b2-4ac<4a2；③a>12；其中正确的个数为（）A.0B.1C.2D.3

Question

如图，二次函数y=ax²+bx+c的图象与x轴交于A、B两点，与y轴交于点C，且OB=OC，下列结论：①b>1且b≠2；②b²-4ac<4a²；③a>

(1)/(2)；其中正确的个数为（　　）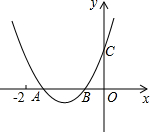

A. 0

B. 1

C. 2

D. 3

Answer 1

①∵OB=OC，
∴C（0，c），B（-c，0）
把B（-c，0）代入y=ax²+bx+c得0=ac²-bc+c，即0=ac²+c（1-b），
∵a>0，
∴1-b<0，即b>1，
如果b=2，由0=ac²-bc+c，可得ac=1，此是△=b²-4ac=0，故b>1且b≠2正确，
②∵a>0，b>0，c>0，设C（0，c），B（-c，0）
∵AB=|x₁-x₂|<2，
∴（x₁+x₂）²-4x₁x₂<4，
∴（-(b)/(a)）²-4×(c)/(a)<4，即(b2)/(a2)-(4c)/(a)<4，
∴b²-4ac<4a²；故本项正确．
③把B（-c，0）代入y=ax²+bx+c可得ac+1=b，
代入y=ax²+bx+c得y=ax²+（ac+1）x+c=ax²+acx+x+c=ax²+x+acx+c=x（ax+1）+c（ax+1）=（x+c）（ax+1），
解得x₁=-c，x₂=-(1)/(a)，
由图可得x₁，x₂>-2，
即-(1)/(a)>-2，
∵a>0，
∴(1)/(a)<2，
∴a>(1)/(2)；正确．
所以正确的个数是3个．
故选：D．