若实数x，y满足x-y≤1x-2y+2≥02x+y≥2则z=x-ay只在点（4，3）处取得最大值，则a的取值范围为（）A.（-∞，0）∪（1，+∞）B.（1，+∞）C.（0，1）D.（-∞，1）

Question

若实数x，y满足

x-y≤1

x-2y+2≥0

2x+y≥2

则z=x-ay只在点（4，3）处取得最大值，则a的取值范围为（　　）

A. （-∞，0）∪（1，+∞）

B. （1，+∞）

C. （0，1）

D. （-∞，1）

Answer 1

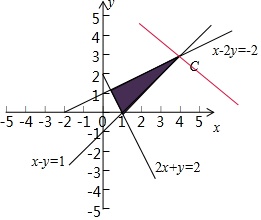由不等式组

x-y≤1

x-2y+2≥0

2x+y≥2

作可行域如图，
联立

x-2y=-2

x-y=1

，解得C（4，3）．
当a=0时，目标函数化为z=x，由图可知，
可行解（4，3）使z=x-ay取得最大值，符合题意；
当a>0时，由z=x-ay，得y=(1)/(a)x-(z)/(a)，此直线斜率大于0，当在y轴上截距最大时z最大，
可行解（4，3）为使目标函数z=x-ay的最优解，
a<1符合题意；
当a<0时，由z=x-ay，得y=(1)/(a)x-(z)/(a)，此直线斜率为负值，
要使可行解（4，3）为使目标函数z=x-ay取得最大值的唯一的最优解，则(1)/(a)<0，即a<0．
综上，实数a的取值范围是（-∞，0）．
故选：D．