设函数f(x)=|x+2|，x≤0|log2x|，x>0若关于x的方程f（x）=a有四个不同的解x1，x2，x3，x4，且x1<x2<x3<x4，则x3（x1+x2）+1x23x4的取值范围是（）A.（-3，+∞）B.（-∞，3）C.[-3，3

Question

设函数f(x)=

|x+2|，   x≤0

|log2x|，  x>0

若关于x的方程f（x）=a有四个不同的解x₁，x₂，x₃，x₄，且x₁<x₂<x₃<x₄，则x₃（x₁+x₂）+(1)/(x23x4)的取值范围是（　　）

A. （-3，+∞）

B. （-∞，3）

C. [-3，3）

D. （-3，3]

Answer 1

作函数f(x)=

|x+2|，   x≤0

|log2x|，  x>0

的图象如下，
，
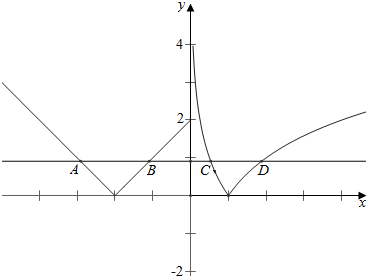结合图象，
A，B，C，D的横坐标分别为x₁，x₂，x₃，x₄，
故x₁+x₂=-4，x₃x₄=1，
故x3(x1+x2)+(1)/(x32x4)=(1)/(x3)-4x₃，
∵0<-log₂x₃≤2，
∴(1)/(4)≤x₃<1，
∴-3<(1)/(x3)-4x₃≤3，
故选：D．