设双曲线x2a2-y2b2=1（a>0，b>0）的左、右焦点分别为F1，F2，以F1为圆心，|F1F2|为半径的圆与双曲线在第一、二象限内依次交于A，B两点，若|F1B|=3|F2A|，则该双曲线的离心率为（）A.54B.
设双曲线
-x2 a2
=1（a>0，b>0）的左、右焦点分别为F1，F2，以F1为圆心，|F1F2|为半径的圆与双曲线在第一、二象限内依次交于A，B两点，若|F1B|=3|F2A|，则该双曲线的离心率为（ ）y2 b2
A. 5 4
B. 4 3
C. 3 2
D. 2
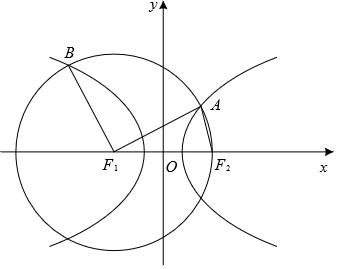根据已知可得，|F1B|=|F1A|=3|F2A|，又|F1A|-|F2A|=2a，∴2|F2A|=2a，即|F2A|=a，
又因为|F1A|=丨F1F2丨=2c，则2c=3a，
∴e=
| c |
| a |
| 3 |
| 2 |
故选：C．
（1）.已知a,b都是正数,且a≠b,求证：2ab／a+b＜（ab的开方）（2）.已知a,b都是正数 2020-03-30 …
已知a(a-1)+(b-a的二次方)=负7,求(2分之a的平方+b的平方)-ab的值a(a-1)+ 2020-05-15 …
高二三角函数题,急,在锐角△ABC中,角A,B,C所对的边分别是a,b,c,已知sinA=(2×2 2020-05-21 …
已知A={1,2,a},B={1,a的二次方},A∪B={1,2,a},求所有可能的a值已知A={ 2020-06-02 …
简算:1.22*2×9－1.33*2×4分解因式:(A+B+C)*2-(A+B-C)*2(X+Y) 2020-06-24 …
﹙a－2﹚^2－6﹙2﹣a）与18（a-b）^3-12b（b-a）^2为何式子一=﹙a－2﹚^2+ 2020-07-30 …
设a>0,b>0且ab-（a+b）≥1则A.a+b≥2（根号二+1）B.a+b≤根号二+1C.a- 2020-07-31 …
二项式看不懂(a+b)^2的展开式=(a+b)(a+b)=a*a+a*b+b*a+b*b=a^2+ 2020-07-31 …
回答下列问题若二次根式√a+8b和9a的a+b次方若二次根式√a+8b和9a的a+b次方是是同类二 2020-08-02 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …