早教吧作业答案频道 -->数学-->
数列{an}是等差数列,Sn是其前n项和(n∈N*),若.(1)求数列{an}的通项公式;(2)设,Tn是数列{bn}的前n项和,求Tn的表达式;(3)设,求C2+C4+C6+…+C2n+2.
题目详情
数列{a n }是等差数列,S n 是其前n项和(n∈N * ),若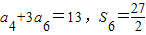 .
.
(1)求数列{a n }的通项公式;
(2)设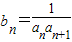 ,T n 是数列{b n }的前n项和,求T n 的表达式;
,T n 是数列{b n }的前n项和,求T n 的表达式;
(3)设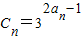 ,求C 2 +C 4 +C 6 +…+C 2n+2 .
,求C 2 +C 4 +C 6 +…+C 2n+2 .
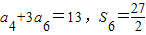 .
.(1)求数列{a n }的通项公式;
(2)设
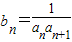 ,T n 是数列{b n }的前n项和,求T n 的表达式;
,T n 是数列{b n }的前n项和,求T n 的表达式;(3)设
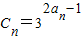 ,求C 2 +C 4 +C 6 +…+C 2n+2 .
,求C 2 +C 4 +C 6 +…+C 2n+2 .▼优质解答
答案和解析
分析:
(1)直接把条件转化为首项和公差来表示,求出首项和公差,即可求出数列{an}的通项公式;(2)直接把上一问的结果代入,求出数列{bn}的通项公式;再利用裂项相消法求出Tn的表达式;(3)先把所求数列{an}的通项公式代入求出=3n,进而得到c2,c4,c6…c2n-2是首项为9,公比为9的等比数列.再代入等比数列的求和公式即可求C2+C4+C6+…+C2n+2.
(1)由已知得:解得:.所以an=1+(n-1)×=.(2)∵==4()∴sn=4[()+()+…+()]=4(-)=.(3)∵=3n,∴c2,c4,c6…c2n-2是首项为9,公比为9的等比数列.∴C2+C4+C6+…+C2n+2=32+34+…+32n+2==.
点评:
本题主要考查等差数列和等比数列的综合问题.解决本题的关键在于求出数列{an}的通项公式以及裂项相消求和的运用.
分析:
(1)直接把条件转化为首项和公差来表示,求出首项和公差,即可求出数列{an}的通项公式;(2)直接把上一问的结果代入,求出数列{bn}的通项公式;再利用裂项相消法求出Tn的表达式;(3)先把所求数列{an}的通项公式代入求出=3n,进而得到c2,c4,c6…c2n-2是首项为9,公比为9的等比数列.再代入等比数列的求和公式即可求C2+C4+C6+…+C2n+2.
(1)由已知得:解得:.所以an=1+(n-1)×=.(2)∵==4()∴sn=4[()+()+…+()]=4(-)=.(3)∵=3n,∴c2,c4,c6…c2n-2是首项为9,公比为9的等比数列.∴C2+C4+C6+…+C2n+2=32+34+…+32n+2==.
点评:
本题主要考查等差数列和等比数列的综合问题.解决本题的关键在于求出数列{an}的通项公式以及裂项相消求和的运用.
看了数列{an}是等差数列,Sn是...的网友还看了以下:
简单的等差数列求法!..1、设{an}是等差数列,若a2=3,a7=13,则数列{an}前8项的和为 2020-03-30 …
有17列人站成的长方形队列,若增加51人则可以站成正方形队列;若减少50人,也可站成正方形队列.求 2020-04-26 …
若一个数列的第m项等于这个数列的前m项的积,则称该数列为“m积数列”若正项等比数列{an}是一个“ 2020-06-30 …
数列{an}为等差数列,{bn}为等比数列.①若a1=2,a10=38数列{an}为等差数列,{b 2020-07-09 …
设数列{an}是首项为1的等比数列,若{1/[2an+a(n+1)]}是等差数列,则(1/2a1+ 2020-07-09 …
对于数列{an},下列说法正确的是()若n≥2,且an+1+an-1=2an,则{an}为等差数列 2020-07-21 …
已知Sn是等差数列{an}的前n项和,bn=Sn/n,①证:数列{bn}是等差数列②若S7=已知S 2020-07-23 …
若a用六列五行,若b用六列九行表示他们的位置,则ab点在同一列,若c用五列五行,d用八列五行表示, 2020-12-15 …
数学问题9人一组,站成三行三列间距为1米的正方形队列,若以其中四人为顶点组成正方形,问这样的正方形有 2020-12-24 …
已知数列{an}的各项为正数,其前n项和为sn(1)若数列{sn/n}是公差为1的等差数列,且a2= 2021-02-09 …