如图，一次函数y=-12x+m（m>0）的图象与x轴、y轴分别交于点A、B，点C在线段OA上，点C的横坐标为n，点D在线段AB上，且AD=2BD，将△ACD绕点D旋转180°后得到△A1C1D．（1）若点C1恰好落在y轴上，

Question

如图，一次函数y=-(1)/(2)x+m（m>0）的图象与x轴、y轴分别交于点A、B，点C在线段OA上，点C的横坐标为n，点D在线段AB上，且AD=2BD，将△ACD绕点D旋转180°后得到△A₁C₁D．

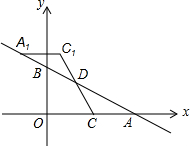
（1）若点C₁恰好落在y轴上，试求(n)/(m)的值；
（2）当n=4时，若△A₁C₁D被y轴分得两部分图形的面积比为3：5，求该一次函数的解析式．

Answer 1

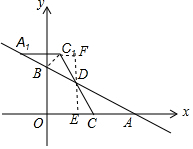（1）由题意，得B（0，m），A（2m，0），
如图，过点D作x轴的垂线，交x轴于点E，交直线A₁C₁于点F，
易知：DE=(2)/(3)m，D（(2)/(3)m，(2)/(3)m），C₁（(4)/(3)m-n，(4)/(3)m），
∴(4)/(3)m-n=0，∴(n)/(m)=(4)/(3)；
（2）由（1）得，当m>3时，点C₁在y轴右侧；当2<m<3时，点C₁在y轴左侧．
①当m>3时，设A₁C₁与y轴交于点P，连接C₁B，
由△A₁C₁D被y轴分得两部分图形的面积比为3：5，∴S△BA₁P：S△BC₁P=3：1，
∴A₁P：C₁P=3，∴(2)/(3)m=3（(4)/(3)m-4），∴m=(18)/(5)，
∴y=-(1)/(2)x+(18)/(7)；
②当2<m<3时，同理可得：y=-(1)/(2)x+(18)/(5)；
综上所述，y=-(1)/(2)x+(18)/(7)或y=-(1)/(2)x+(18)/(5)．