早教吧作业答案频道 -->数学-->
如图,已知长方体ABCD-A1B1C1D1,AB=2,AD=1,AA1=2,P是棱A1B1上任意一点,Q是侧面对角线AB1上一点,则PD1+PQ的最小值是()A.3B.322C.5D.1+2
题目详情
如图,已知长方体ABCD-A1B1C1D1,AB=2,AD=1,AA1=2,P是棱A1B1上任意一点,Q是侧面对角线AB1上一点,则PD1+PQ的最小值是( )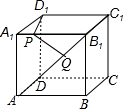
A. 3
B. 3 2 2
C. 5
D. 1+2
▼优质解答
答案和解析
将正方形展开,取A1B1C1D1及ABB1A1两个面,过点D1作D1Q⊥AB1于点Q,D1Q交A1B1于点P,此时PD1+PQ取最小值D1Q.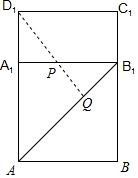
∵ABB1A1为正方形,
∴∠D1AQ=45°.
在Rt△D1QA中,AD1=AA1+A1D1=3,∠D1QA=90°,∠D1AQ=45°,
∴D1Q=sin∠D1AQ•AD1=
.
故选B.

∵ABB1A1为正方形,
∴∠D1AQ=45°.
在Rt△D1QA中,AD1=AA1+A1D1=3,∠D1QA=90°,∠D1AQ=45°,
∴D1Q=sin∠D1AQ•AD1=
3
| ||
| 2 |
故选B.
看了如图,已知长方体ABCD-A1...的网友还看了以下:
一个矩形的对角线长10cm,一边长6cm,则其周长是,面积是. 2020-03-30 …
一根长12cm的秒针,半分钟扫过钟面的面积是()小园半径是大圆半径的1/4,则小圆面积是大圆面积的几 2020-03-30 …
长方形的面积是24dm,长是6dm,面积与长方形的最简单整数比是(),比值是(). 2020-03-31 …
一条线段AB长度是a(a大于0),C是线段AB上的一点,线段AC长是线段AB与CB的长的比例中项, 2020-04-27 …
一个矩形的对角线长10cm,一边长6cm,则其周长是,面积是. 2020-05-20 …
菱形的对角线长分别为6和8,则菱形的边长是,面积是. 2020-05-23 …
线与面平行,则线所在的面与这个面平行?是线面平行转换为面面平行吗? 2020-06-06 …
已知菱形的两条对角线的差是2,周长为20,求这个菱形的面积.一个长方形的周长是18cm,面积是20 2020-06-26 …
菱形的两条对角线分别为12和16,则菱形的边长是,面积是. 2020-07-06 …
菱形的两条对角线分别为12和16,则菱形的边长是,面积是. 2020-07-06 …