早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,以对角线AC、BD的交点O为位似中心,解答以下问题:(1)按新图与已知图形的相似比为12和2作两个矩形A1B1C1D1和A2B2C2D2(2)求△0A1B1和四边形A1D1D2A2的面积之比.
题目详情
如图,在矩形ABCD中,以对角线AC、BD的交点O为位似中心,解答以下问题:
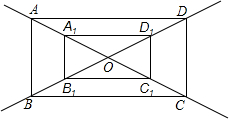
(1)按新图与已知图形的相似比为
和2作两个矩形A1B1C1D1和A2B2C2D2
(2)求△0A1B1和四边形A1D1D2A2的面积之比.

(1)按新图与已知图形的相似比为
| 1 |
| 2 |
(2)求△0A1B1和四边形A1D1D2A2的面积之比.
▼优质解答
答案和解析
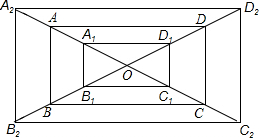 (1)如图所示:矩形A1B1C1D1和矩形A2B2C2D2,即为所求;
(1)如图所示:矩形A1B1C1D1和矩形A2B2C2D2,即为所求;
(2)∵新图与已知图形的相似比为
和2,
∴
=
,
∴
=
,
∵矩形A1B1C1D1,
∴S△OA1B1=S△OA1D1,
∴△0A1B1和四边形A1D1D2A2的面积之比为:1:15.
 (1)如图所示:矩形A1B1C1D1和矩形A2B2C2D2,即为所求;
(1)如图所示:矩形A1B1C1D1和矩形A2B2C2D2,即为所求;(2)∵新图与已知图形的相似比为
| 1 |
| 2 |
∴
| A1D1 |
| A2D2 |
| 1 |
| 4 |
∴
| S△OD1A1 |
| S△A2OD2 |
| 1 |
| 16 |
∵矩形A1B1C1D1,
∴S△OA1B1=S△OA1D1,
∴△0A1B1和四边形A1D1D2A2的面积之比为:1:15.
看了如图,在矩形ABCD中,以对角...的网友还看了以下:
方阵,则是()A)上三角矩阵B)下三角矩阵C)对称矩阵D)可逆矩阵 2020-05-13 …
高等代数的证明题设A是实数域上的n级可逆矩阵,证明:A可以分解成A=TB,其中T是正交矩阵,B是上 2020-05-13 …
●假设一个6阶的下三角矩阵B按列优先顺序压缩存储在一维数组A中,其中A[0]存储矩阵的第一个元素b1 2020-05-25 …
假设一个6阶的下三角矩阵B按列优先顺序压缩存储在一维数组A中,其中A[0]存储矩阵的第二个元素b11 2020-05-26 …
A,B均为n阶正交矩阵,且A^TB+B^TA+E≠0,则A.AB,A+B都是正交矩阵B.AB是正交 2020-06-18 …
关于对称阵对角化一般可逆矩阵和正交阵都能使对称阵对角化那么这里的可逆矩阵和正交阵有什么关系呢?是不 2020-06-18 …
如图,将两张长为5,宽为一的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两 2020-06-19 …
2、设矩阵A=2-1-1,-12-1,-1-12,2、设矩阵A=2-1-1,-12-1,-1-12 2020-06-30 …
求出特征向量a123.用X=[a1,a2,a3]Y就能化二次型为标准型了,为什么还要正交变换为r12 2020-12-02 …
以前老师解过这样一道题,有些地方没弄懂二次型f的矩阵A=1b1ba1111相似于对角矩阵B=diag 2020-12-19 …