如图，已知CO1是△ABC的中线，过点O1作O1E1∥AC交BC于点E1，连接AE1交CO1于点O2；过点O2作O2E2∥AC交BC于点E2，连接AE2交CO1于点O3；过点O3作O3E3∥AC交BC于点E3，…，如此继续，可以依次得到点O4，O5

Question

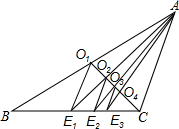
如图，已知CO₁是△ABC的中线，过点O₁作O₁E₁∥AC交BC于点E₁，连接AE₁交CO₁于点O₂；过点O₂作O₂E₂∥AC交BC于点E₂，连接AE₂交CO₁于点O₃；过点O₃作O₃E₃∥AC交BC于点E₃，…，如此继续，可以依次得到点O₄，O₅，…，O_n和点E₄，E₅，…，E_n．则O_nE_n=___AC．（用含n的代数式表示）

Answer 1

解∵O₁E₁∥AC，
∴△BO₁E₁∽△BAC，
∴(O1E1)/(AC)=(BO1)/(AB)，
∵O₁是AB的中点，
∴BO₁=(1)/(2)AB，
∴(O1E1)/(AC)=(1)/(2)，
∴O₁E₁=(1)/(2)AC，
∵O₁E₁∥AC，
∴△O₁E₁O₂∽△CAO₂，
∴(O1E1)/(AC)=(E1O2)/(E1A)=(1)/(2)，
∴(E1O2)/(E1A)=(1)/(3)，
∵O₂E₂∥AC，
∴△E₁O₂E₂∽△E₁AC，
∴(O2E2)/(AC)=(E1O2)/(E1A)=(1)/(3)，
∴O₂E₂=(1)/(3)AC，
同理得：(O3E3)/(AC)=(E2O3)/(E2A)=(1)/(4)，
O₃E₃=(1)/(4)AC，
…
∴O_nE_n=(1)/(n+1)AC，
故答案为：(1)/(n+1)．