如图，△ABC、△CDE都是等边三角形，且点A、C、E在一条直线上，AD与BE、AD与BC、BE与CD分别交于点O、点P、点Q．求证：（1）AD=BE，AP=BQ；（2）∠AOB=60°，OC平分∠AOE；（3）PQ∥AE；（4）△CPQ为

Question

如图，△ABC、△CDE都是等边三角形，且点A、C、E在一条直线上，AD与BE、AD与BC、BE与CD分别交于点O、点P、点Q．求证：

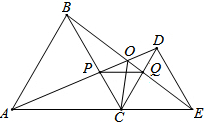
（1）AD=BE，AP=BQ；
（2）∠AOB=60°，OC平分∠AOE；
（3）PQ∥AE；
（4）△CPQ为等边三角形；
（5）(1)/(PQ)=(1)/(AC)+(1)/(CE)．

Answer 1

证明：（1）∵△ABC和△CDE都是等边三角形，
∴AC=BC，CE=CD，∠ACB=∠ECD=60°，
∴∠ACB+∠ACE=∠ECD+∠ACE，
即∠BCE=∠ACD，
在△BCE和△ACD中，

BC=AC

∠BCE=∠ACD

CE=CD

，
∴△BCE≌△ACD（SAS），
∴AD=BE，∠CAP=∠BCQ，
在△ACP和△BCQ中，

∠BCQ=∠ACP

AC=BC

∠CAP=∠CBQ

，
∴△ACP≌△BCQ（ASA），
∴AP=BQ；
（2）∵∠AOB+∠ABO+∠BAO=180°，∠OBC=∠CAO
∴∠AOB+∠ABC+∠BAC=180°，
∴∠AOB=60°，
∵∠EOD+∠EDO+∠OED=180°，
∴∠ODC+∠DEO=60°，
∴∠ODC=∠CEO，
同理∠OCD=∠DEO，
∴∠COE=60°，
∴OC平分∠AOE；
（3）∵∠PQD+∠DPQ+∠PDQ=180°，
∵∠DPQ=∠DEO，∠PDQ=∠CEO，
∴∠DPQ+∠PDQ=60°
∴∠PQD=∠ACD=120°，
∴PQ∥AE，
（4）∵PQ∥AE
∴∠CPQ=∠ACB=60°，
∵∠PCQ=60°，
∴△CPQ为等边三角形；
（5）∵PQ∥AE，
∴(QP)/(AC)=(DQ)/(CD)=(CD-QC)/(CD)，
∵CD=CE，CQ=PQ，
∴(QP)/(AC)=(CE-PQ)/(CE)，(QP)/(AC)=1-(PQ)/(CE)，
两边同时除PQ得(1)/(PQ)=(1)/(AC)+(1)/(CE)．