早教吧作业答案频道 -->数学-->
如图,△ABC中,AB=AC,∠BAC=90°,BC=4,线段MN在BC边上沿BC方向运动(运动开始时,点M与点B重合,点N到达点C时运动终止),MN=1,分别过点M、N分别作BC的垂线,与折线B→A→C交于P、Q两点,设
题目详情
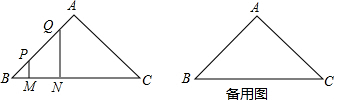
如图,△ABC中,AB=AC,∠BAC=90°,BC=4,线段MN在BC边上沿BC方向运动(运动开始时,点M与点B重合,点N到达点C时运动终止),MN=1,分别过点M、N分别作BC的垂线,与折线B→A→C交于P、Q两点,设线段BM的长为x.
(1)线段MN在运动的过程中,当PM=QN时,求x值;
(2)线段MN在运动的过程中,PM+QN=y,请用含x的式子表示y,并写出x的取值范围.
(1)线段MN在运动的过程中,当PM=QN时,求x值;
(2)线段MN在运动的过程中,PM+QN=y,请用含x的式子表示y,并写出x的取值范围.

▼优质解答
答案和解析
(1)如图1,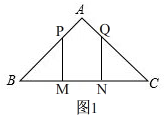 在△ABC中,AB=AC,∠BAC=90°,
在△ABC中,AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵PM⊥BC,QN⊥BC,
∴∠PMB=∠QNC=90°,
在Rt△PMB中,PM=BM,
同理:QN=CN,
∵PM=QN,
∴BM=CN,
∵BC=4,MN=1,
∴BC=BM+MN+CN=2BM+MN=4,
∴BM=
(4-MN)=
,
∴x=
;
(2)①、如图2,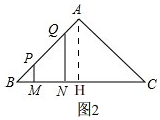 在等腰直角三角形ABC中,BC=4,
在等腰直角三角形ABC中,BC=4,
∴BH=CH=
BC=2,
∵MN=1,
∴BM<1
当0≤x≤1时,
在Rt△OMB中,∠ABC=45°,
∴PM=BM=x,
在Rt△QNB中,QN=BN=BM+MN=x+1,
∴y=PM+QN=x+x+1=2x+1,
②、如图3,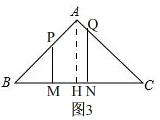 当1<x<2时,同①得,PM=BM=x,
当1<x<2时,同①得,PM=BM=x,
在Rt△QNC中,QN=CN,
∵BC=BM+MN+CN,
∴QN=CN=BC-BM-MN=4-x-1=3-x,
∴y=PM+QN=x+3-x=3;
③、如图4,当2≤x≤3时,
∵BC=4,BM=x,
∴CM=BC-BM=4-x,
∵MN=1,
∴CN=CM-MN=4-x-1=3-x,
在Rt△PMC中,PM=CM=4-x,
同理:QN=CN=3-x,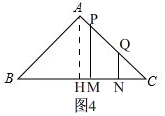
∴y=PM+QN=4-x+3-x=7-2x;
即:y=
.
 在△ABC中,AB=AC,∠BAC=90°,
在△ABC中,AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,
∵PM⊥BC,QN⊥BC,
∴∠PMB=∠QNC=90°,
在Rt△PMB中,PM=BM,
同理:QN=CN,
∵PM=QN,
∴BM=CN,
∵BC=4,MN=1,
∴BC=BM+MN+CN=2BM+MN=4,
∴BM=
| 1 |
| 2 |
| 3 |
| 2 |
∴x=
| 3 |
| 2 |
(2)①、如图2,
 在等腰直角三角形ABC中,BC=4,
在等腰直角三角形ABC中,BC=4,∴BH=CH=
| 1 |
| 2 |
∵MN=1,
∴BM<1
当0≤x≤1时,
在Rt△OMB中,∠ABC=45°,
∴PM=BM=x,
在Rt△QNB中,QN=BN=BM+MN=x+1,
∴y=PM+QN=x+x+1=2x+1,
②、如图3,
 当1<x<2时,同①得,PM=BM=x,
当1<x<2时,同①得,PM=BM=x,在Rt△QNC中,QN=CN,
∵BC=BM+MN+CN,
∴QN=CN=BC-BM-MN=4-x-1=3-x,
∴y=PM+QN=x+3-x=3;
③、如图4,当2≤x≤3时,
∵BC=4,BM=x,
∴CM=BC-BM=4-x,
∵MN=1,
∴CN=CM-MN=4-x-1=3-x,
在Rt△PMC中,PM=CM=4-x,
同理:QN=CN=3-x,

∴y=PM+QN=4-x+3-x=7-2x;
即:y=
|
看了如图,△ABC中,AB=AC,...的网友还看了以下:
在平面直角坐标系与向量中有不懂的问题三角形ABC中,AB等于5,AC等于5,BC等于6,内角平分线 2020-06-03 …
设向量OM=M向量a,向量ON=N向量b,向量OP=α向量a+β向量b,且向量a与向量b不共线其中 2020-06-06 …
设向量a,b是不共线的两个非零向量,向量OM=m向量a,向量ON=n向量b,向量OP=α向量aβ向 2020-06-06 …
一个高中数学题 要全解已知椭圆方程(x^2/3b^2)+(y^2/b^2)=1 (b>0),经过椭 2020-06-27 …
向量比值问题已知向量OA=1,向量OB=根号3,向量OA点乘向量OB=0,点C在角AOC上角AOC 2020-07-19 …
设函数f(x)=m向量×n向量,其中向量m=(2cosx,1),n向量=(cosx庚号3sin2x 2020-07-21 …
设A,B,C三点满足向量OC=m*向量OA+n*向量OB,其中O是不在直线AB上的一点,证明A,B 2020-07-24 …
在△ABC中,AB=2,BC=根号10,AC=3,设点O为△ABC的外心,若向量AO=m向量AB+ 2020-07-30 …
已知点A(1,1)B(2,3)C(3,2)点p(x,y)在△ABC三边围成的区域(含边界)上1)若 2020-07-31 …
已知向量OA的模=1,向量OB的模=根号2,向量OA垂直于向量OB,点C在角AOB内,且角AOB=4 2020-12-18 …