早教吧作业答案频道 -->数学-->
正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.(1)证明:△ABM∽△MCN;(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长;(3)设BM=x,当M点运
题目详情
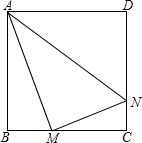
正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
(1)证明:△ABM∽△MCN;
(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长;
(3)设BM=x,当M点运动到什么位置时△ABM∽△AMN,求x的值.

(1)证明:△ABM∽△MCN;
(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长;
(3)设BM=x,当M点运动到什么位置时△ABM∽△AMN,求x的值.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=4,∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,
∴Rt△ABM∽Rt△MCN.
(2)∵△ABM∽△MCN,△ABM的周长与△MCN周长之比是4:3,
∴
=
=
,
∴
=
,
∴MC=3,
∴BM=4-3=1,
∴
=
,
∴NC=
(3) ∵∠B=∠AMN=90°,
∴要使△ABM∽△AMN,则有
=
,
由(1)知
=
,
∴
=
,
∴BM=MC,
∴当点M运动到BC的中点时,△ABM∽△AMN,此时,x=2.
∴AB=BC=CD=4,∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠MAB+∠AMB=90°,
∴∠CMN=∠MAB,
∴Rt△ABM∽Rt△MCN.
(2)∵△ABM∽△MCN,△ABM的周长与△MCN周长之比是4:3,
∴
| BM |
| NC |
| AB |
| MC |
| 4 |
| 3 |
∴
| 4 |
| MC |
| 4 |
| 3 |
∴MC=3,
∴BM=4-3=1,
∴
| 1 |
| NC |
| 4 |
| 3 |
∴NC=
| 3 |
| 4 |
(3) ∵∠B=∠AMN=90°,
∴要使△ABM∽△AMN,则有
| AM |
| MN |
| AB |
| BM |
由(1)知
| AM |
| MN |
| AB |
| MC |
∴
| AB |
| BM |
| AB |
| MC |
∴BM=MC,
∴当点M运动到BC的中点时,△ABM∽△AMN,此时,x=2.
看了正方形ABCD边长为4,M,N...的网友还看了以下:
乙醇厌氧过程的化学方程式参考式子:CnHaOb+(n-a/4-b/2)H2O=(n/2-a/8+b 2020-05-13 …
近代化学基础急一1.在用量子数表示核外电子运动状态时,写出下列各组中所缺少的量子数.(1)n=3, 2020-06-04 …
1.对于任何有理数n,多项式(4n+5)^2-9能被...A被8整除B被n整除C被2n+7整除D被 2020-06-11 …
求和4^n+3*4^n-1+3^2*4^n-2+……+3^n-1*4+3^n(n∈n*) 2020-07-09 …
等比数列{an}的前n项和Sn=2^n-1,则a1^2+a2^2+a3^2+...+an^2=前n 2020-07-30 …
1.下列各式中,形如a^2±2ab+b^2形式的多项式有()①a^2-a+1/4②x^2+xy+y 2020-07-31 …
数学归纳法求证1/2+2/2^2+3/2^3+4/2^4+…+n/5^n=2-(n+2)/2^n( 2020-08-01 …
无穷数列an中,a1=1,an=√(an-1)^2+4,(n>=2,n属于N*)已知数列{an}中 2020-08-02 …
1、设全集为U=Z集合A={xlx=2n,n属于Z}B={xlx=2n+1,n属于Z},求Ca,Cb 2020-10-31 …
期待您的回答数列un=((2n)!n^(1/2))/((n!)^2*4^n),求证ln(un)有界, 2020-11-05 …