已知二次函数y=ax2+bx+c（a≠0）与x轴一个交点在-1，-2之间，对称轴为直线x=1，图象如图，给出以下结论：①b2-4ac>0；②abc>0；③2a-b=0；④8a+c<0；⑤a+13b+19c<0．其中结论正确的个数有（

Question

已知二次函数y=ax²+bx+c（a≠0）与x轴一个交点在-1，-2之间，对称轴为直线x=1，图象如图，给出以下结论：①b²-4ac>0；②abc>0；③2a-b=0；④8a+c<0；⑤a+

(1)/(3)b+(1)/(9)c<0．其中结论正确的个数有（　　）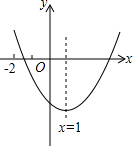

A. 1

B. 2

C. 3

D. 4

Answer 1

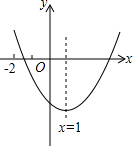∵抛物线与x轴有两个交点，
∴b²-4ac>0，①正确；
∵抛物线开口向上，
∴a>0，
∵对称轴在y轴的右侧，
∴b<0，
∵抛物线与y轴交于负半轴，
∴c<0，
∴abc>0，②正确；
∵-(b)/(2a)=1，∴2a+b=0，③错误；
∵x=-2时，y>0，
∴4a-2b+c>0，即8a+c>0，④错误；
根据抛物线的对称性可知，当x=3时，y<0，
∴9a+3b+c<0，
∴a+(1)/(3)b+(1)/(9)c<0，⑤正确．
综上所述，正确的结论是：①②⑤．
故选：C．