早教吧作业答案频道 -->物理-->
如图所示,质量m=0.5kg的小球从距地面高H=5m处自由下落,到达地面A点时恰能沿凹陷于地面的粗糙半圆形槽壁运动,半圆槽半径R=0.4m.小球到达槽最低点时的速率为vB=10m/s,并继续沿槽壁运动
题目详情
如图所示,质量m=0.5kg的小球从距地面高H=5m处自由下落,到达地面A点时恰能沿凹陷于地面的粗糙半圆形槽壁运动,半圆槽半径R=0.4m.小球到达槽最低点时的速率为vB=10m/s,并继续沿槽壁运动直至从槽左端边缘飞出,竖直上升,落下后恰好又沿槽壁运动直到从槽右端边缘飞出,竖直上升、下落,如此反复几次.设粗糙半圆形槽壁对小球的摩擦力大小恒定不变.求:
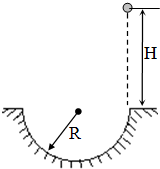
(1)小球开始下落后,第一次到达A点时的速度大小vA;
(2)小球第一次离槽上升高度h;
(3)小球最多能飞出槽外几次?(g=10m/s2)

(1)小球开始下落后,第一次到达A点时的速度大小vA;
(2)小球第一次离槽上升高度h;
(3)小球最多能飞出槽外几次?(g=10m/s2)
▼优质解答
答案和解析
(1)小球开始下落到第一次到达A点的过程机械能守恒,则有:
mgH=
m
代入数据解得:vA=10m/s
(2)小球从高处至槽口时,只有重力做功;由槽口至槽底端重力、摩擦力都做功.由于对称性,圆槽右半部分摩擦力的功与左半部分摩擦力的功相等.小球落至槽底部的整个过程中,由动能定理得:
mg(H+R)-Wf=
mvB2;
解得:Wf=mg(H+R)-
mvB2=0.5×10×(5+0.4)-
×0.5×102=2J;
由对称性知,小球从槽底到槽左端口克服摩擦力做功也为2J,设小球第一次离槽上升的高度为h,从最低点到左侧最高点的过程,由动能定理得:
-mg(h+R)-Wf=0-
mvB2;
代入数据解得:h=4.2m
(3)设小球飞出槽外n次,对整个过程,由动能定理得:mgH-n×2Wf=0
解得:n=
=6.25,n只能取整数,故小球最多能飞出槽外6次.
答:(1)小球开始下落后,第一次到达A点时的速度大小vA是10m/s
(2)小球第一次离槽上升高度h为4.2m;
(3)小球最多能飞出槽外6次.
mgH=
| 1 |
| 2 |
| v | 2 A |
代入数据解得:vA=10m/s
(2)小球从高处至槽口时,只有重力做功;由槽口至槽底端重力、摩擦力都做功.由于对称性,圆槽右半部分摩擦力的功与左半部分摩擦力的功相等.小球落至槽底部的整个过程中,由动能定理得:
mg(H+R)-Wf=
| 1 |
| 2 |
解得:Wf=mg(H+R)-
| 1 |
| 2 |
| 1 |
| 2 |
由对称性知,小球从槽底到槽左端口克服摩擦力做功也为2J,设小球第一次离槽上升的高度为h,从最低点到左侧最高点的过程,由动能定理得:
-mg(h+R)-Wf=0-
| 1 |
| 2 |
代入数据解得:h=4.2m
(3)设小球飞出槽外n次,对整个过程,由动能定理得:mgH-n×2Wf=0
解得:n=
| mgH |
| 2Wf |
答:(1)小球开始下落后,第一次到达A点时的速度大小vA是10m/s
(2)小球第一次离槽上升高度h为4.2m;
(3)小球最多能飞出槽外6次.
看了如图所示,质量m=0.5kg的...的网友还看了以下:
图示地区为我国某地的地质剖面图和地表地貌剖面图,图中数字表示的是地层编号(1-5表示地层年代有老到 2020-05-01 …
如图所示是对二氧化碳性质的探究.完成下列填空:如图所示,将二氧化碳气体慢慢倒入烧杯中,可观察到的现 2020-05-13 …
归纳是重要的学习方法,小红在复习盐酸的性质是,归纳出盐酸的五条化学性质(如图所示,连线表示相互反应 2020-05-15 …
归纳是学习的重要方法,小红在复习盐酸的性质时,归纳出盐酸的五条化学性质(如图所示,连线表示相互反应 2020-06-11 …
自然界的氧循环自然界中的物质循环,形成了自然界中物质的平衡.如图是氧在自然界的主要循环途径.请认真 2020-06-13 …
某温度时,在体积为2L的密闭容器中,气态物质A、B、E、F的物质量n随时间t的变化如图甲所示,在一 2020-06-14 …
简谐横波在均匀介质中沿直线传播,P、Q是传播方向上相距10m的两质点,波先传到P,当波传到Q开始计 2020-06-19 …
进出口贸易实务多选题表示品质的方法有()表示品质的方法有()A凭样品表示商品的品质B平实物表示商品 2020-06-20 …
如图所示,一个容积为450ml、质量是0.5kg的瓶子里装有200cm3的水.乌鸦为了喝到瓶子里的 2020-06-20 …
20℃时,根据某固体物质在不同质量的水中达到饱和状态时溶解的质量绘成如图斜线,结合图示进行分析,下 2020-06-25 …