早教吧作业答案频道 -->数学-->
如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3)(1)求抛物线的解析式.(2)设抛物线与x轴的负半轴交于点C,在直线y=-x+5有一点E,使△A
题目详情
如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3)
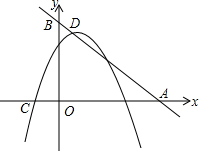
(1)求抛物线的解析式.
(2)设抛物线与x轴的负半轴交于点C,在直线y=-x+5有一点E,使△ABO与△ACE相似,求出点E的坐标.
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点P,使△APC的面积等于△ACE的面积?如果存在,请求出点P的坐标;如果不存在,请说明理由.

(1)求抛物线的解析式.
(2)设抛物线与x轴的负半轴交于点C,在直线y=-x+5有一点E,使△ABO与△ACE相似,求出点E的坐标.
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点P,使△APC的面积等于△ACE的面积?如果存在,请求出点P的坐标;如果不存在,请说明理由.
▼优质解答
答案和解析
(1)设抛物线的顶点坐标为(t,-t+5),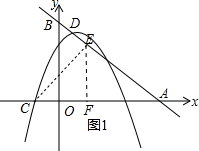
则抛物线解析式为y=-(x-t)2-t+5,
把(2,3)代入得-(2-t)2-t+5=3,
整理得t2-3t+2=0,解得t1=1,t2=2(舍去),
所以抛物线解析式为y=-(x-1)2-1+5,即y=-x2+2x+3;
(2)当x=0时,y=-x+5=5,则B(0,5);当y=0时,-x+5=0,解得x=5,则A(5,0),
当y=0时,-x2+2x+3,解得x1=1,x2=3,则C(-1,0),
∵OA=OB=5,
∴△AOB为等腰直角三角形,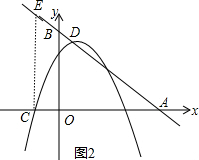
∴∠BAO=45°,
作CF⊥AB于F,如图1,则△ACE为等腰直角三角形,△AOB∽△ACE,
∴EF=
AC=
(5+1)=3,
∴E点坐标为(2,3),
过点C作CE⊥x轴交直线y=-x+5于E点,如图2,当x=-1时,y=-x+5=6,则E(-1,6),
∵CE∥OB,
∴△AOB∽△ACE,
综上所述,点E的坐标为(-1,6)或(2,3);
(3)存在.
设P(x,-x2+2x+3),
当E(2,3)时,S△ACE=
×6×3=9,
∵△APC的面积等于△ACE的面积,
∴
•6•(x2-2x-3)=9,解得x1=1+
,x2=1-
,
此时P点坐标为(1+
,-3)或(1-
,-3);
当E(-1,6)时,S△ACE=
×6×6=18,
∵△APC的面积等于△ACE的面积,
∴
•6•(x2-2x-3)=18,解得x1=1+
,x2=1-
,
此时P点坐标为(1+
,-3)或(1-

则抛物线解析式为y=-(x-t)2-t+5,
把(2,3)代入得-(2-t)2-t+5=3,
整理得t2-3t+2=0,解得t1=1,t2=2(舍去),
所以抛物线解析式为y=-(x-1)2-1+5,即y=-x2+2x+3;
(2)当x=0时,y=-x+5=5,则B(0,5);当y=0时,-x+5=0,解得x=5,则A(5,0),
当y=0时,-x2+2x+3,解得x1=1,x2=3,则C(-1,0),
∵OA=OB=5,
∴△AOB为等腰直角三角形,

∴∠BAO=45°,
作CF⊥AB于F,如图1,则△ACE为等腰直角三角形,△AOB∽△ACE,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴E点坐标为(2,3),
过点C作CE⊥x轴交直线y=-x+5于E点,如图2,当x=-1时,y=-x+5=6,则E(-1,6),
∵CE∥OB,
∴△AOB∽△ACE,
综上所述,点E的坐标为(-1,6)或(2,3);
(3)存在.
设P(x,-x2+2x+3),
当E(2,3)时,S△ACE=
| 1 |
| 2 |
∵△APC的面积等于△ACE的面积,
∴
| 1 |
| 2 |
| 7 |
| 7 |
此时P点坐标为(1+
| 7 |
| 7 |
当E(-1,6)时,S△ACE=
| 1 |
| 2 |
∵△APC的面积等于△ACE的面积,
∴
| 1 |
| 2 |
| 10 |
| 10 |
此时P点坐标为(1+
| 10 |
|
作业帮用户
2017-01-27
举报
举报该用户的提问
举报类型(必填)
举报理由(必填) 0/100
提交

 |
看了如图,直线y=-x+5与x、y...的网友还看了以下:
将两小球同时从地面竖直上抛,A上升的比B高出35m,返回地面的时间比B迟2s求两球的初速度各为多少 2020-04-26 …
将2个小石块从地面上同时竖直上抛,A上升最大高度比B的最大高度高35米,返回地面比B迟2秒,求(1 2020-04-26 …
将两个小球同时竖直上抛,A上升的最大高度比B上升的最大高度高出35m,返回抛出点的时间比B迟2s. 2020-04-26 …
关系矩阵的问题,没学过,突然要考模拟试题,请各位帮忙分析下面的简答题设集合A={a,b,c,d}, 2020-05-13 …
从一个点A向斜上方与水平面成θ角方向抛掷一个物体B,初速度为V,抛到C点,C点的高度与A点差为H( 2020-05-14 …
将两个小球同时竖直上抛,a上升的最大高度比b上升的最大高度高出35m,返回地面时间比b迟2s,问: 2020-05-21 …
已知线段AB=10,点P在线段AB上,且AP=6,以A为圆心AP为半径作⊙A,点C在⊙A上,以B为 2020-06-08 …
设集合A={a,b,c,d},A上的二元关系R={,,,}(1)求出r(R),s(R),t(R)( 2020-06-12 …
将两个小球同时竖直上抛,A上升的最大高度比B上升的最大高度高出35米,返回地面时间比B迟了2秒,试 2020-06-22 …
直线ab的公垂线段,AB=2cm,a,b所成的角为90度,A、C在a上,B、D在b上,AC=4cm 2020-06-27 …
 扫描下载二维码
扫描下载二维码