已知函数f(x)=x3+ax2+bx+1的图象为D.(1)当a=b=3时过D上的点P(tf(t))(-1＜t＜0)作D的切线与x轴、y轴分别交于A、B求△ABO面积的最大值(O为坐标原点);(2)当a=0时D与x轴有三个不同的交点试

Question

已知函数f(x)=x ³ +ax ² +bx+1的图象为D.

(1)当a=b=3时 过D上的点P(t f(t))(-1＜t＜0)作D的切线与x轴、y轴分别交于A、B 求△ABO面积的最大值(O为坐标原点);

(2)当a=0时 D与x轴有三个不同的交点 试求b的取值范围.

Answer 1

解:(1)∵f(x)=(x+1) ³ ∴f′(x)=3(x+1) ² .故过P的切线方程为y-(t+1) ³ =3(t+1) ² (x-t).

它在两坐标轴上的截距分别为y ₀ =(1+t) ³ -3t(1+t) ² =(1+t) ² (1-2t)，

x ₀ =t .故S _△ABO = |(1+t) ² ·(1-2t)· |

= ［（2+2t)(1-2t)］ ² ≤ .( ) ⁴ = .当t= 时取等号.

故S _△ABO 的最大值为 .

(2)a=0时 f(x)=x ³ +bx+1 f′(x)=3x ² +b

b≥0时 f′(x)≥0 y=f(x)为增函数 D与x轴只有一个交点 结论不成立.

b＜0时 令f′(x)=0.求得x= 时 f(x)极大值=f( )= +1.

x= 时 f(x)极小值=f( )= +1.

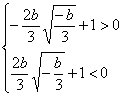
图象D与x轴有三个不同的交点 b ³ +1＜0 b＜ .

因此b的取值范围是(-∞ ).