早教吧作业答案频道 -->数学-->
如图,二次函数y=a(x+1)2+2的图象与x轴交于A,B两点,已知A(-3,0),根据图象回答下列问题.(1)求a的值和点B的坐标;(2)设抛物线的顶点是P,试求△PAB的面积;(3)在抛物线上是
题目详情
如图,二次函数y=a(x+1)2+2的图象与x轴交于A,B两点,已知A(-3,0),根据图象回答下列问题.
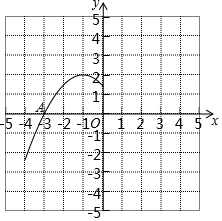
(1)求a的值和点B的坐标;
(2)设抛物线的顶点是P,试求△PAB的面积;
(3)在抛物线上是否存在点M,使得△MAB的面积等于△PAB的面积的2倍?若存在,求出点M的坐标.
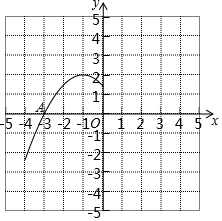
(1)求a的值和点B的坐标;
(2)设抛物线的顶点是P,试求△PAB的面积;
(3)在抛物线上是否存在点M,使得△MAB的面积等于△PAB的面积的2倍?若存在,求出点M的坐标.
▼优质解答
答案和解析
(1)将(-3,0)代入y=a(x+1)2+2,
可得0=4a+2,解得a=-
;
∵抛物线对称轴方程为x=-1,A、B两点关于对称轴对称,
∴B的坐标为(1,0),
(2)∵y=-
(x+1)2+2,
∴抛物线的顶点坐标是(-1,2),
∵A(-3,0),B(1,0),
∴AB=XB-XA=1-(-3)=4,
∴S△PAB=
×4×2=4.
(3)S△MAB=
×4×|yM|=2 S△PAB=8
∴|yM|=4,∴yM=±4,
当yM=4时,y=-
(x+1)2+2=4,无解.
当yM=-4时,y=-
(x+1)2+2=-4,
解得x=-1±2
∴M(-1+2
,-4)或M(-1-2
,-4)
可得0=4a+2,解得a=-
| 1 |
| 2 |
∵抛物线对称轴方程为x=-1,A、B两点关于对称轴对称,
∴B的坐标为(1,0),
(2)∵y=-
| 1 |
| 2 |
∴抛物线的顶点坐标是(-1,2),
∵A(-3,0),B(1,0),
∴AB=XB-XA=1-(-3)=4,
∴S△PAB=
| 1 |
| 2 |
(3)S△MAB=
| 1 |
| 2 |
∴|yM|=4,∴yM=±4,
当yM=4时,y=-
| 1 |
| 2 |
当yM=-4时,y=-
| 1 |
| 2 |
解得x=-1±2
| 3 |
∴M(-1+2
| 3 |
| 3 |
看了如图,二次函数y=a(x+1)...的网友还看了以下:
设双曲线C的中点在原点,点A(2根号3/3,0)为右焦点,X=根号3/6为右准线设l:y=kx+1 2020-04-08 …
线性代数问题:已知三阶方阵A的行列式|A|=3,求A的伴随矩阵的逆(A*)-1的值.答案我知道是A 2020-04-13 …
已知函数f(x)=x^3+x-16.直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切 2020-05-20 …
1、判断正误.(1){a}∈{{a}}(2){a}⊆{{a}}(3){a}∈{{a},a}(4){ 2020-07-09 …
一题数学题:设A为三阶矩阵,α1,α2,α3是线性无关的三维列设A为三阶矩阵,α1,α2,α3是线 2020-07-14 …
设α1,α2,α3为4元非齐次线性方程组Ax=β的3个解,r(A)=3且α1+α2=(2,-4,0 2020-08-02 …
若a为第二象限角,则a/2为第几象限角?a/3呢?答案上说求a/2时设k=2n和k=2n+1,a/ 2020-08-03 …
英语翻译我用EVEREST测的结果是AnalogDevicesAD1985@Intel82801EB 2020-10-31 …
1.设3阶方阵A的行列式|A|=1/2,则|A^3|=2..设向量a=(1,2,3,4),则a的单位 2020-11-02 …
数学,线性代数,设A是方阵,A的k次方=0,k为正整数,求I+A+(A^2)/2!+(A^3)/.. 2020-11-20 …