早教吧作业答案频道 -->数学-->
如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,(1)试判断△PMN的形状;(2)连接MN,设直线y=x交MN于点G,若PG:PN=3:4,△PGN的周长为6,求△PON
题目详情
如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,
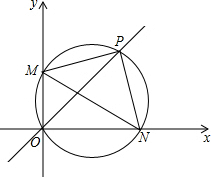
(1)试判断△PMN的形状;
(2)连接MN,设直线y=x交MN于点G,若PG:PN=3:4,△PGN的周长为6,求△PON的周长.

(1)试判断△PMN的形状;
(2)连接MN,设直线y=x交MN于点G,若PG:PN=3:4,△PGN的周长为6,求△PON的周长.
▼优质解答
答案和解析
(1) △PMN是等腰直角三角形,
理由:∵y=x,
∴∠PON=∠POM=45°.
∴PN=PM.
∵四边形ONPM内接于圆,
∴∠MON+∠NPM=180°.
∵∠MON=90°,
∴∠NPM=90°.
即△PMN是等腰直角三角形.
(2)∵△PMN是等腰直角三角形,
∴∠PMN=∠PNM
∵∠OPN=∠OPN,
∴△PNG∽△PON.
∴△PNG的周长:△PON的周长=PG:PN=3:4.
∴△PNG的周长=6,
∴△PON的周长=8.
理由:∵y=x,
∴∠PON=∠POM=45°.
∴PN=PM.
∵四边形ONPM内接于圆,
∴∠MON+∠NPM=180°.
∵∠MON=90°,
∴∠NPM=90°.
即△PMN是等腰直角三角形.
(2)∵△PMN是等腰直角三角形,
∴∠PMN=∠PNM
∵∠OPN=∠OPN,
∴△PNG∽△PON.
∴△PNG的周长:△PON的周长=PG:PN=3:4.
∴△PNG的周长=6,
∴△PON的周长=8.
看了如图:M、N分别为直角坐标系x...的网友还看了以下:
已知二次函数y=ax²+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )x … -1 2020-05-16 …
过双曲线x方比a方—y方比b方=1的右焦点f做一条垂直于x轴的直线,交双曲线于ab两点若线断ab的 2020-05-20 …
已知圆C过点P(2,-2)与直线X-Y=O相切,且圆心在直线X+Y=O上,问(1)求圆C的标准方程 2020-05-23 …
如图,在△ABC中,∠B与∠C的平分线教育点P,设∠A=x°,∠BPC=y°当∠A变化时求y与x的 2020-06-04 …
判断下列各对直线是否相交,若相交,求出交点坐标(1)L1:x-2y=0,L2:2x-y+1=0(2 2020-07-25 …
如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.(1)求抛物线顶点A的坐标;(2)设 2020-07-30 …
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.已知曲线C:x=cosθy=-1+ 2020-07-31 …
知道双曲线的渐近线是Y=2X时怎么判断双曲线的焦点在Y轴还是在X轴?已知双曲线X2+aY2=1的渐 2020-08-01 …
已知曲线C1:y^2/4+x^2=1与曲线(要具体回答)已知曲线C1:y^2/4+x^2=1与曲线C 2020-10-31 …
(2012•宜宾)如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.(1)求抛物线顶点A 2020-11-12 …