早教吧作业答案频道 -->数学-->
已知P,Q,R是抛物线y=x2上不同的三点,设P,Q的横坐标分别为a,a+1(a>0),R与Q是关于y轴对称的两点.(1)求△PQR的面积S关于a的关系式;(2)当△PQR的面积S等于28时,求a的值.
题目详情
已知P,Q,R是抛物线y=x2上不同的三点,设P,Q的横坐标分别为a,a+1(a>0),R与Q是关于y轴对称的两点.
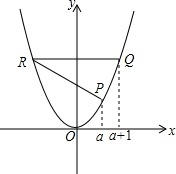
(1)求△PQR的面积S关于a的关系式;
(2)当△PQR的面积S等于28时,求a的值.

(1)求△PQR的面积S关于a的关系式;
(2)当△PQR的面积S等于28时,求a的值.
▼优质解答
答案和解析
(1)∵R与Q是关于y轴对称的两点,
∴RQ=2(a+1),
把点P,Q的横坐标分别代入抛物线y=x2中,
得到点P(a,a2),点Q(a+1,(a+1)2),
(a+1)2-a2=2a+1,
∴S=
×2(a+1)(2a+1)=2a2+3a+1;
(2)由题意得2a2+3a+1=28,
解得:a=3或a=-
(舍去)
答:a的值是3.
∴RQ=2(a+1),
把点P,Q的横坐标分别代入抛物线y=x2中,
得到点P(a,a2),点Q(a+1,(a+1)2),
(a+1)2-a2=2a+1,
∴S=
| 1 |
| 2 |
(2)由题意得2a2+3a+1=28,
解得:a=3或a=-
| 9 |
| 2 |
答:a的值是3.
看了已知P,Q,R是抛物线y=x2...的网友还看了以下:
在一个坐标系中,点p与点p`关于Y轴对称,已知点p(-sin30度,cos30度)求点p`的坐标: 2020-05-04 …
如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(-4,0),点B的坐标为(0,b)(b>0) 2020-05-16 …
如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(-4,0),点B的坐标为(0,b)(b>0) 2020-05-16 …
在平面直角坐标系xOy中,点P的坐标为(a,b),点P的“变换点”P′的坐标定义如下:当a≥b时, 2020-06-19 …
已知:抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧),顶点为P.(1)求A、 2020-07-26 …
已知点p,q关于直线x=1对称点p的横坐标是-3点q纵坐标为-2已知点p,q关于直线x=1对称点p 2020-08-01 …
(2006•盐城)已知:抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧),顶点为 2020-11-12 …
(2006•盐城)已知:抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧),顶点为 2020-11-12 …
坐标系中的坐标点坐标点怎么有实心的和空心的? 2020-12-25 …
,已知点P和点Q是曲线y=x^2-2x-3上的两点,且点P的横坐标是1,点Q的横坐标是4,求(1)知 2021-02-07 …