早教吧作业答案频道 -->数学-->
如图,反比例函数y1=kx的图象与一次函数y2=14x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1=kx的图象上.(1)求反比例函数的表达式;(2)观察图象回答:当x为何范围时
题目详情
如图,反比例函数y1=
的图象与一次函数y2=
x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1=
的图象上.
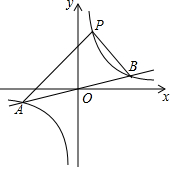
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.
| k |
| x |
| 1 |
| 4 |
| k |
| x |

(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.
▼优质解答
答案和解析
(1)把x=4代入y2=
x,得到点B的坐标为(4,1),
把点B(4,1)代入y1=
,得k=4.
反比例函数的表达式为y1=
;
(2)∵点A与点B关于原点对称,
∴A的坐标为(-4,-1),
观察图象得,当x<-4或0<x<4时,y1>y2;
(3)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,
设AP与y轴交于点C,如图,
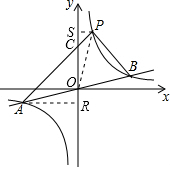 ∵点A与点B关于原点对称,
∵点A与点B关于原点对称,
∴OA=OB,
∴S△AOP=S△BOP,
∴S△PAB=2S△AOP.
y1=
中,当x=1时,y=4,
∴P(1,4).
设直线AP的函数关系式为y=mx+n,
把点A(-4,-1)、P(1,4)代入y=mx+n,
则
,
解得
.
故直线AP的函数关系式为y=x+3,
则点C的坐标(0,3),OC=3,
∴S△AOP=S△AOC+S△POC
=
OC•AR+
OC•PS
=
×3×4+
×3×1
=
,
∴S△PAB=2S△AOP=15.
| 1 |
| 4 |
把点B(4,1)代入y1=
| k |
| x |
反比例函数的表达式为y1=
| 4 |
| x |
(2)∵点A与点B关于原点对称,
∴A的坐标为(-4,-1),
观察图象得,当x<-4或0<x<4时,y1>y2;
(3)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,
设AP与y轴交于点C,如图,
 ∵点A与点B关于原点对称,
∵点A与点B关于原点对称,∴OA=OB,
∴S△AOP=S△BOP,
∴S△PAB=2S△AOP.
y1=
| 4 |
| x |
∴P(1,4).
设直线AP的函数关系式为y=mx+n,
把点A(-4,-1)、P(1,4)代入y=mx+n,
则
|
解得
|
故直线AP的函数关系式为y=x+3,
则点C的坐标(0,3),OC=3,
∴S△AOP=S△AOC+S△POC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 15 |
| 2 |
∴S△PAB=2S△AOP=15.
看了如图,反比例函数y1=kx的图...的网友还看了以下:
已知集合A={X|X≤2},B={X|X>A}(1)若A交于B=∅,求A的取值范围(2)若A∪B= 2020-06-03 …
磁感线不能相交是因为什么磁感线不能相交是因为()A在磁场中任何位置只有一个磁场,因此磁感线是不能相 2020-06-08 …
聪明人解答:已知抛物线y=x平方-2(k-1)x+k平方-7与x轴有两个不同的交点已知抛物线y=x 2020-06-14 …
如图,表示抛物线y=ax2+bx+c的一部分图象,它与x轴的一个交点为A,与y轴交于B,则b的取值 2020-06-29 …
分速度的方向可能与速度成90度角吗,所成交的范围是?答得好补充20分 2020-07-09 …
1、“转基因技术造成的变异,相当与基因重组,是认为制造的定向变异"这句话是对的,可我不明白为什么是 2020-07-25 …
设集合A={x|1<x<2},B={x|x<a},若A真包含于B,则实数a的范围是2.已知集合A= 2020-08-02 …
集合A(-1,1),集合B(b-a,a+b),a=1是A交B的充分条件,求b的范围求高手们快帮帮小 2020-08-02 …
男女同学要适度交往,这要求我们在交往中()A.真诚相待,彼此尊重B.既不过分夸张,也不闪烁其词C.既 2020-11-11 …
价值规律要求的等价交换是指A.每一次具体的交换过程都是等价交换B.等价交换的实现有赖于价格依据供求变 2020-11-21 …