如图，在平面直角坐标系中，已知A（a，0），B（0，b）两点，且a、b满足（3a-2b）2+|a-b-1|=0，点C（m，0）在x轴的正半轴上，将线段AB平移到DC，连接对应点A、D和B、C，请回答下列问题：（1）

Question

如图，在平面直角坐标系中，已知A（a，0），B（0，b）两点，且a、b满足（3a-2b）²+|a-b-1|=0，点C（m，0）在x轴的正半轴上，将线段AB平移到DC，连接对应点A、D和B、C，请回答下列问题：

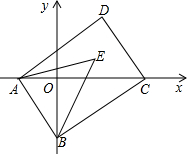
（1）求A、B两点的坐标；
（2）设四边形ABCD的面积满足9<S_{四边形ABCD}<15，求m的取值范围；
（3）分别作∠OAD、∠OBC的平分线AE、BE，交点为E，请直接写出∠AEB的度数（不必说明理由）．

Answer 1

（1）∵（3a-2b）²+|a-b-1|=0，
∴3a-2b=0，a-b-1=0，
∴a=-2，b=-3，
∴A（-2，0），B（0，-3）；
（2）∵B（0，-3），
∴OB=3，
∵将线段AB平移到DC，连接对应点A、D和B、C，
∴S_△ABC=S_△ADC，
∴S_{四边形ABCD}=2S_△ABC=2×(1)/(2)AC×OB=3m，
∵9<S_{四边形ABCD}<15，
∴9<3m<15，
∴3<m<5；
（3）由平移得，AD∥BC，
∴∠DAB+∠CBA=180°，
∴∠DAC+∠OAB+∠ABO+∠OBC=180°，
∵∠OAB+∠ABO=90°，
∴∠DAC+∠OBC=90°，
∵∠OAD、∠OBC的平分线AE、BE，交点为E，
∴2∠EAC=∠DAC，2∠CBE=∠CBO，
∴∠EAC+∠CBE=45°，
∵∠OAB+∠ABO=90°，
∴∠EAB+∠EBA=90°+45°=135°，
∴∠AEB=180°-（∠EAB+∠EBA）=180°-135°=45°．