早教吧作业答案频道 -->数学-->
已知,等腰△ABC,AB=AC(1)如图1,BM是△ABC的中线,点N在BM上,且∠ANM=∠MBC,求证:BC=AN;(2)如图2,点G为外一点,∠BGC=∠BAC,AH⊥BG于H,若BH=7,HG=1,求线段CG的长;(3)如图3,等腰△A
题目详情
已知,等腰△ABC,AB=AC
(1)如图1,BM是△ABC的中线,点N在BM上,且∠ANM=∠MBC,求证:BC=AN;
(2)如图2,点G为外一点,∠BGC=∠BAC,AH⊥BG于H,若BH=7,HG=1,求线段CG的长;
(3)如图3,等腰△ABC和等腰△ADE共顶点A,AD=AE,顶角∠DAE=∠BAC,点F是线段BE和CD的交点,连AF,请写出∠AFC与∠ADE之间的等量关系,并证明你的结论.
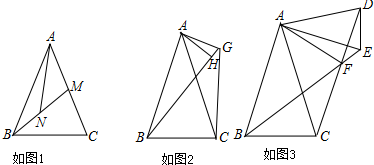
(1)如图1,BM是△ABC的中线,点N在BM上,且∠ANM=∠MBC,求证:BC=AN;
(2)如图2,点G为外一点,∠BGC=∠BAC,AH⊥BG于H,若BH=7,HG=1,求线段CG的长;
(3)如图3,等腰△ABC和等腰△ADE共顶点A,AD=AE,顶角∠DAE=∠BAC,点F是线段BE和CD的交点,连AF,请写出∠AFC与∠ADE之间的等量关系,并证明你的结论.

▼优质解答
答案和解析
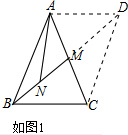 (1)如图1,延长BM至点D,使DM=BM,
(1)如图1,延长BM至点D,使DM=BM,
∵AM=CM,
∴四边形ABCD是平行四边形,
∴AD=BC,∠DBC=∠ADB,
∵∠ANM=∠DBC,
∴∠ANM=∠ADB,
∴AN=AD,
∴BC=AN;
(2)如图2,延长CG,过点A作AM⊥CG于点M,
∵AH⊥BG,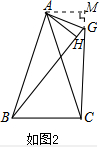
∴∠AHB=∠AMC,
∵∠BAC=∠BGC,
∴∠ABH=∠ACM,
在△CMA和△BHA中,
,
∴△CMA≌△BHA(AAS),
∴CM=BH=7,AM=AH,
在Rt△AMG和△Rt△AHG中,
,
∴△AMG≌△AHG(HL),
∴GM=GH=1,
∴CG=CM-GM=7-1=6,
(3)如图3,设AE与DF交于点M,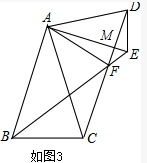
∵∠DAE=∠BAC,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD,
∴A、B、C、F四点共圆,
∴∠ABC+∠AFC=180°,
∴∠ADE=∠ABC,
∴∠ADE+∠AFC=180°.
 (1)如图1,延长BM至点D,使DM=BM,
(1)如图1,延长BM至点D,使DM=BM,∵AM=CM,
∴四边形ABCD是平行四边形,
∴AD=BC,∠DBC=∠ADB,
∵∠ANM=∠DBC,
∴∠ANM=∠ADB,
∴AN=AD,
∴BC=AN;
(2)如图2,延长CG,过点A作AM⊥CG于点M,
∵AH⊥BG,

∴∠AHB=∠AMC,
∵∠BAC=∠BGC,
∴∠ABH=∠ACM,
在△CMA和△BHA中,
|
∴△CMA≌△BHA(AAS),
∴CM=BH=7,AM=AH,
在Rt△AMG和△Rt△AHG中,
|
∴△AMG≌△AHG(HL),
∴GM=GH=1,
∴CG=CM-GM=7-1=6,
(3)如图3,设AE与DF交于点M,

∵∠DAE=∠BAC,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
|
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD,
∴A、B、C、F四点共圆,
∴∠ABC+∠AFC=180°,
∴∠ADE=∠ABC,
∴∠ADE+∠AFC=180°.
看了已知,等腰△ABC,AB=AC...的网友还看了以下:
有关图例和注记的说法,错误的是()A.图例一般附在地图上B.地图上的文字说明属于注记C.地图中的符 2020-05-13 …
“上北下南、左西右东”这一测定方向的方法,应在下列哪一种情况下适用()A.有指向标的地图上B.有经 2020-05-14 …
“上北下南、左西右东”这一测定地图方向的方法,应在下列哪一种情况下适用()A.有指向标的地图上B. 2020-05-14 …
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之 2020-05-16 …
如图,华庆号船位于航海图上平面直角坐标系中的点A(10,2)处时,点C、海岛B的位置在y轴上,且∠ 2020-06-23 …
如图为一突触的结构,在a、d两点连接一个灵敏电流计.已知ab=bd,若分别刺激b、c两点,灵敏电流 2020-07-07 …
关于图例和注记,正确的是()A.图例是地图上各种文字说明B.图例就是表示各种地理事物的符号C.在不 2020-07-10 …
如图(甲)所示,A车原来临时停在一水平路面上,B车在后面匀速向A车靠近,A车司机发现后启动A车,以 2020-07-22 …
如图A、B是某种雌性动物细胞分裂示意图,C表示该动物细胞分裂过程中核DNA含量变化曲线。请据图回答问 2020-11-02 …
qjp163如图(图式这样的C是水平地面,AB是两长方体物块,A在上B在下很简单的一个图)F是作用在 2020-11-07 …