早教吧作业答案频道 -->数学-->
在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.(1)如图①,若∠BAC=60°,则按边分
题目详情
在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
(1)如图①,若∠BAC=60°,则按边分类:△CEF是___三角形;
(2)若∠BAC<60°.
①如图②,当点D在线段CB上移动时,判断△CEF的形状并证明;
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请在图③中画出相应的图形并直接写出结论(不必证明).
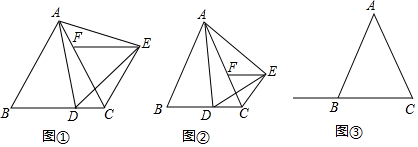
(1)如图①,若∠BAC=60°,则按边分类:△CEF是___三角形;
(2)若∠BAC<60°.
①如图②,当点D在线段CB上移动时,判断△CEF的形状并证明;
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请在图③中画出相应的图形并直接写出结论(不必证明).

▼优质解答
答案和解析
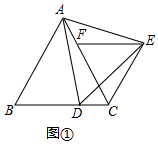 (1)如图1,∵AB=AC,AD=AE,∠BAC=∠DAE=60°,
(1)如图1,∵AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠ACB=∠ABC=60°,∠EAC=∠DAB,
∴△DAB≌△EAC,
∴∠ECA=∠B=60°,
∵EF∥BC,
∴∠EFC=∠ACB=60°,
∵在△EFC中,∠EFC=∠ECF=60°=∠CEF,
∴△EFC为等边三角形,
故答案为:等边;
(2)①△CEF为等腰三角形,
证明:如图2,∵AB=AC,AD=AE,∠BAC=∠DAE,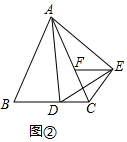
∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠B,
∴∠ACE=∠ACB,
∵EF∥BC,
∴∠EFC=∠ACB,
∴∠EFC=∠ACE,
∴CE=FE,
∴△EFC为等腰三角形;
②如图③,△EFC为等腰三角形.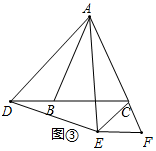
当点D在BC延长线上时,以AD为一边在AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线EF,交直线AC的延长线于点F,连接DE.
证明:∵AB=AC,AD=AE,∠BAC=∠DAE,
∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECF=∠ABC,
∵EF∥BC,
∴∠AFE=∠ACB,
又∵∠ABC=∠ACB,
∴∠AFE=∠ECF,
∴EC=EF,
∴△EFC为等腰三角形.
 (1)如图1,∵AB=AC,AD=AE,∠BAC=∠DAE=60°,
(1)如图1,∵AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠ACB=∠ABC=60°,∠EAC=∠DAB,
∴△DAB≌△EAC,
∴∠ECA=∠B=60°,
∵EF∥BC,
∴∠EFC=∠ACB=60°,
∵在△EFC中,∠EFC=∠ECF=60°=∠CEF,
∴△EFC为等边三角形,
故答案为:等边;
(2)①△CEF为等腰三角形,
证明:如图2,∵AB=AC,AD=AE,∠BAC=∠DAE,

∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠B,
∴∠ACE=∠ACB,
∵EF∥BC,
∴∠EFC=∠ACB,
∴∠EFC=∠ACE,
∴CE=FE,
∴△EFC为等腰三角形;
②如图③,△EFC为等腰三角形.

当点D在BC延长线上时,以AD为一边在AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线EF,交直线AC的延长线于点F,连接DE.
证明:∵AB=AC,AD=AE,∠BAC=∠DAE,
∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECF=∠ABC,
∵EF∥BC,
∴∠AFE=∠ACB,
又∵∠ABC=∠ACB,
∴∠AFE=∠ECF,
∴EC=EF,
∴△EFC为等腰三角形.
看了在△ABC中,AB=AC,点D...的网友还看了以下:
小四数学题,急等.要分析过程:三个字母A、B、C按下面的规律排成一列:A、B、B、C、B、C、A、 2020-06-03 …
为什么金刚石中每个碳原子形成四个C-C键金刚石中由共价键构成的最小环有6个碳原子每个环平均拥有:1 2020-06-07 …
c/c++数据结构一元多项式的求和一个一元多项式可以看作由若干个一元单项式按降幂排列成的线性表.请 2020-06-27 …
如图,△ABC绕点C按顺时针方向旋转57°后得到△DEC,如果DC⊥BC,那么∠A+∠B等于()A 2020-07-18 …
1)设a=19^96,b=96^19,c=199^6,d=6^199,则此四数按从小到大的顺序排列 2020-07-18 …
在极坐标系中,若等边三角形ABC(顶点A,B,C按顺时针方向排列)的顶点A,B的极坐标分别为(2, 2020-08-02 …
关于平衡常数的问题我们知道有aA+bBcC+dD(C(C))^c*(C(D)^d)k=------- 2020-10-30 …
C/C++谁做了好事一个同学做了件好事,没有留名。A说:不是我。B说:是C。C说:是D。D说:C胡说 2020-11-04 …
右图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→ 2020-11-23 …
在一固定容积密闭容器内,2molA和1molB在一定条件下发生反应:2A(g)+B(g)=3C(g) 2020-11-29 …