早教吧作业答案频道 -->数学-->
如图,点E、M分别是正方形ABCD边的AB、CD上的动点,连结DE,过M作MF⊥DE于H,交AD于点F.(1)如图1,当点M与点C重合,点E与点A、B不重合时.①求证:△DAE≌△CDF;②连结BH,当点E运动到什么
题目详情
如图,点E、M分别是正方形ABCD边的AB、CD上的动点,连结DE,过M作MF⊥DE于H,交AD于点F.
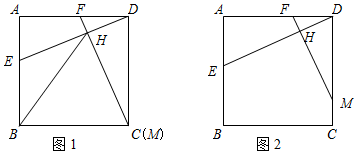
(1)如图1,当点M与点C重合,点E与点A、B不重合时.
①求证:△DAE≌△CDF;
②连结BH,当点E运动到什么位置时,BH=BC?
(2)如图2,若正方形ABCD边长为3cm,点E从点A出发,以1.5cm/秒的速度沿边AB向点B运动,同时,点M从点C出发,以1cm/秒的速度沿边CD向点D运动.设运动时间为t秒(0<t<2),否存在这样的t,使CM=DF,若存在,求出t的值;若不存在,请说明理由.

(1)如图1,当点M与点C重合,点E与点A、B不重合时.
①求证:△DAE≌△CDF;
②连结BH,当点E运动到什么位置时,BH=BC?
(2)如图2,若正方形ABCD边长为3cm,点E从点A出发,以1.5cm/秒的速度沿边AB向点B运动,同时,点M从点C出发,以1cm/秒的速度沿边CD向点D运动.设运动时间为t秒(0<t<2),否存在这样的t,使CM=DF,若存在,求出t的值;若不存在,请说明理由.
▼优质解答
答案和解析
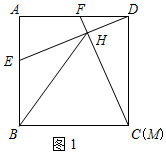 证明:(1)①如图1,∵四边形ABCD是正方形,
证明:(1)①如图1,∵四边形ABCD是正方形,
∴AD=DC,∠A=∠FDC=90°,
∴∠CDH+∠ADE=90°,
∵CF⊥DE,
∴∠CDH+∠FCD=90°,
∴∠ADE=∠FCD,
∴△DAE≌△CDF(ASA);
②如图2,延长DE交CB的延长线于G,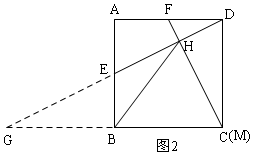
若BH=BC,
则∠BCH=∠BHC,
∵∠CHG=90°,
∴∠G+∠BCH=90°,
∠GHB+∠BHC=90°,
∴∠G=∠GHB,
∴BG=BH=BC=AD,
∵∠A=∠ABG=90°,AD∥BC,
∴∠ADE=∠G,
∴△DAE≌△GBE(ASA),
∴AE=BE,
∴当E运动到中点时,BH=BC;
(2)存在,
如图3,由题意得:AE=1.5t,CM=t,则DM=3-t,
∵∠ADE=∠FMD,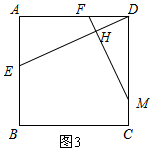
∠A=∠FDC,
∴△ADE∽△DMF,
∴
=
,
∴
=
,
∴DF=
(3-t),
若CM=DF,
则t=
(3-t),
解得t1=1,t2=0(舍),
∴当t=1时,CM=DF.
 证明:(1)①如图1,∵四边形ABCD是正方形,
证明:(1)①如图1,∵四边形ABCD是正方形,∴AD=DC,∠A=∠FDC=90°,
∴∠CDH+∠ADE=90°,
∵CF⊥DE,
∴∠CDH+∠FCD=90°,
∴∠ADE=∠FCD,
∴△DAE≌△CDF(ASA);
②如图2,延长DE交CB的延长线于G,

若BH=BC,
则∠BCH=∠BHC,
∵∠CHG=90°,
∴∠G+∠BCH=90°,
∠GHB+∠BHC=90°,
∴∠G=∠GHB,
∴BG=BH=BC=AD,
∵∠A=∠ABG=90°,AD∥BC,
∴∠ADE=∠G,
∴△DAE≌△GBE(ASA),
∴AE=BE,
∴当E运动到中点时,BH=BC;
(2)存在,
如图3,由题意得:AE=1.5t,CM=t,则DM=3-t,
∵∠ADE=∠FMD,

∠A=∠FDC,
∴△ADE∽△DMF,
∴
| DF |
| DM |
| AE |
| AD |
∴
| DF |
| 3-t |
| 1.5t |
| 3 |
∴DF=
| t |
| 2 |
若CM=DF,
则t=
| t |
| 2 |
解得t1=1,t2=0(舍),
∴当t=1时,CM=DF.
看了如图,点E、M分别是正方形AB...的网友还看了以下:
这些题目要自己画图的哦.不好意思啦!1已知:直线AB、CD相交于点O,OE平分角BOC,已知角AO 2020-05-13 …
已知集合M={-3,-2,-1,0,1,2,},若a,b属于M,平面直角坐标系内点P的坐标是(a, 2020-05-16 …
如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,点B到a、b的距离分别 2020-07-09 …
已只直线y=1/2x与双曲线y=k/x(k>0)交A,B2点,且A的横坐标为4求1k的值2若双曲线 2020-07-12 …
直线a,b是异面直线,A,B,C为直线a上三点,D,E,F是直线b上三点,A',B',C',D', 2020-07-31 …
已知椭圆x^2/a^2+y^2/b^2=1的左右两个焦点分别为F1F2,右顶点为A,上顶点为B,P 2020-07-31 …
(1)A为直线a外一点,B是直线a上一点,点A到直线a的距离为3厘米,则线段AB的长度的取值范围是 2020-08-01 …
已知圆A的圆心A的坐标是(3,0),圆A的半径为5,点BCDEFG的坐标分别是B(0,-4),C( 2020-08-01 …
已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直 2020-11-02 …
(2009•仙桃)如图,把图中的⊙A经过平移得到⊙O(如左图),如果左图中⊙A上一点P的坐标为(m, 2020-11-13 …