早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ABC=90°,过点B作AC的平行线交∠CAB的平分线于点D,过点D作AB的平行线交AC于点E,交BC于点F,连接BE,交AD于点G.(1)求证:四边形ABDE是菱形;(2)若BD=14,cos∠GBH=78,
题目详情
如图,在△ABC中,∠ABC=90°,过点B作AC的平行线交∠CAB的平分线于点D,过点D作AB的平行线交AC于点E,交BC于点F,连接BE,交AD于点G.
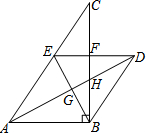
(1)求证:四边形ABDE是菱形;
(2)若BD=14,cos∠GBH=
,求GH的长.

(1)求证:四边形ABDE是菱形;
(2)若BD=14,cos∠GBH=
| 7 |
| 8 |
▼优质解答
答案和解析
(1)证明:∵AC∥BD,AB∥ED,
∴四边形ABDE是平行四边形,
∵AD平分∠CAB,
∴∠CAD=∠BAD,
∵AC∥BD,
∴∠CAD=∠ADB,
∴∠BAD=∠ADB,
∴AB=BD,
∴四边形ABDE是菱形;
(2) ∵∠ABC=90°,
∴∠GBH+∠ABG=90°,
∵AD⊥BE,
∴∠GAB+∠ABG=90°,
∴∠GAB=∠GBH,
∵cos∠GBH=
,
∴cos∠GAB=
,
∴
=
=
,
∵四边形ABDE是菱形,BD=14,
∴AB=BD=14,
∴AH=16,AG=
,
∴GH=AH-AG=
.
∴四边形ABDE是平行四边形,
∵AD平分∠CAB,
∴∠CAD=∠BAD,
∵AC∥BD,
∴∠CAD=∠ADB,
∴∠BAD=∠ADB,
∴AB=BD,
∴四边形ABDE是菱形;
(2) ∵∠ABC=90°,
∴∠GBH+∠ABG=90°,
∵AD⊥BE,
∴∠GAB+∠ABG=90°,
∴∠GAB=∠GBH,
∵cos∠GBH=
| 7 |
| 8 |
∴cos∠GAB=
| 7 |
| 8 |
∴
| AB |
| AH |
| AG |
| AB |
| 7 |
| 8 |
∵四边形ABDE是菱形,BD=14,
∴AB=BD=14,
∴AH=16,AG=
| 49 |
| 4 |
∴GH=AH-AG=
| 15 |
| 4 |
看了如图,在△ABC中,∠ABC=...的网友还看了以下:
直线y=kx+b与直线y=2/1x+3交点的纵坐标是5,而与直线y=3x-9的交点横坐标也是5,则 2020-05-13 …
如图,在直角坐标系中,以点M(3,0)为圆心,以6为半径的圆分别交x轴的正半轴于点A,交x轴的负半 2020-06-14 …
圆的计算题回答者+30分哦圆:r半径d直径c周长s面积r=12s=d=2.4c=c=62.8d=r 2020-07-18 …
已知抛物线y=-316(x-1)(x-9)与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于 2020-07-19 …
如图,已知△ABC,∠ACB=90°,AC<BC,点D为AB的中点,过点D作BC的垂线,垂足为点F 2020-07-31 …
4×9×25=(4×25)×9运用了()A.乘法交换律B.乘法结合律C.乘法分配律D.乘法交换律和 2020-07-31 …
125×(9×8)=9×(125×8)是运用了()A.乘法交换律B.乘法结合律C.加法交换律D.乘 2020-07-31 …
已知AB为圆的直径,CD垂直AB与圆交于C,垂足为D,以C为圆心,CD为半径作圆与前圆交于EF,EF 2020-11-27 …
数学题在线解答已知集合A={三角形},B={等腰三角形},C={等边三角形},D={直角三角形},那 2020-11-27 …
24.以下符合C语言语法的赋值表达式是()。A.a=9+b+c=d+924.以下符合C语言语法的赋值 2020-12-31 …