如图1，在△ABC中，∠C=90°，线段AD，BE是△ABC的两条角平分线，AD与BE相交于点F（1）求证：∠AFE=45°；（2）如图2，过点F作GH⊥BE，GH分别与线段AB，BC相交于点G，H，试判断EF与FH的数量关系，

Question

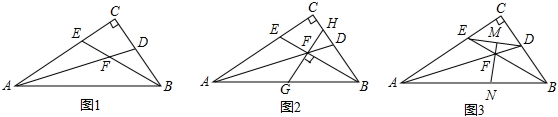
如图1，在△ABC中，∠C=90°，线段AD，BE是△ABC的两条角平分线，AD与BE相交于点F
（1）求证：∠AFE=45°；
（2）如图2，过点F作GH⊥BE，GH分别与线段AB，BC相交于点G，H，试判断EF与FH的数量关系，井说明理由；
（3）如图3，连接DE，点M是线段DE的中点，连接MF，并延长与AB相交于点N，若FM=(5)/(2)，且△DEF的面积为15，求线段FN的长．

Answer 1

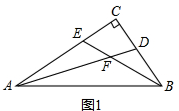证明：（1）如图1，∵∠C=90°，
∴∠CAB+∠CBA=90°，
∵AD、BE是△ABC的两条角平分线，
∴∠DAB=(1)/(2)∠CAB，∠FBA=(1)/(2)∠CBA，
∴∠DAB+∠FBA=(1)/(2)（∠CAB+∠CBA）=(1)/(2)×90°=45°，
∵∠AFE=∠DAB+∠FBA，
∴∠AFE=45°；
（2）如图2，EF=FH，理由是：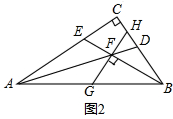
∵∠GFB=∠HFB=90°，BF=BF，∠CBE=∠ABE，
∴△GBF≌△HBF，
∴FH=FG，
由（1）得：∠AFE=45°，
∴∠AFG=90°-45°=45°，
∴∠AFE=∠AFG，
∵∠CAD=∠BAD，AF=AF，
∴△AFE≌△AFG，
∴EF=FG，
∴EF=FH；
（3）如图3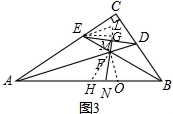，在AB上取两点H、O，使AE=AH，BO=BD，连接FH、FO，
得△AEF≌△AHF，则∠AFH=∠AFE=45°，
同理得：∠BFD=∠BFO=45°，
∴∠HFO=180°-45°-45°-45°=45°，
延长FM至L，使LM=FM，连接EL，
得△EML≌△DMF，则EL=DF，∠LEM=∠FDM，
∵∠BFD=∠FED+∠FDM=45°，
∴∠FED+∠LEM=45°，
即∠LEF=45°，
∴∠LEF=∠HFO=45°，
∵EF=FH，OF=FD=EL，
∴△LEF≌△OFH，
∴∠EFM=∠FHN，
过E作EG⊥MN，交NM的延长线于点G，
∵∠GEF+∠EFG=90°，∠EFG+∠HFN=90°，
∴∠GEF=∠HFN，
∴△EGF≌△FNH，
∴EG=FN，
∵M是DE的中点，
∴S_△DEF=2S_△EFM=2×(1)/(2)FM•EG=FM•EG=15，
∵FM=(5)/(2)，
∴EG=6，
∴FN=EG=6．