早教吧作业答案频道 -->数学-->
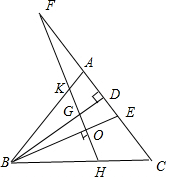
如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论中正确的结论有.①∠DBE=∠F;②∠F=∠BAC-∠C;③2∠BEF=∠BAF+∠C;④∠BGH=∠ABE+∠C
题目详情
如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论中正确的结论有___.
①∠DBE=∠F;②∠F=∠BAC-∠C;
③2∠BEF=∠BAF+∠C;④∠BGH=∠ABE+∠C.
①∠DBE=∠F;②∠F=∠BAC-∠C;
③2∠BEF=∠BAF+∠C;④∠BGH=∠ABE+∠C.

▼优质解答
答案和解析
∵∠FDG=∠BOG,∠AGD=∠BGO,
∴∠F=∠OBG,即∠DBE=∠F,故①正确.
∵BO平分∠ABC,BO⊥HF,易证△BHK是等腰三角形,
∴∠BKH=∠BHK,
∵∠BHK=∠C+∠F,
∴∠F=∠BKH-∠C,
显然∠BKH≠∠BAC,故②错误,
∵∠BAF=∠ABC+∠C=2∠EBC+∠C,
∴∠BAF+∠C=2(∠EBC+∠C)=2∠BEF,故③正确,
∵∠BGH+∠DGH=180°,∠DGH+∠DEO=180°,
∴∠BGH=∠DEO=∠EBC+∠C=∠ABE+∠C,故④正确,
故答案为①③④
∴∠F=∠OBG,即∠DBE=∠F,故①正确.

∵BO平分∠ABC,BO⊥HF,易证△BHK是等腰三角形,
∴∠BKH=∠BHK,
∵∠BHK=∠C+∠F,
∴∠F=∠BKH-∠C,
显然∠BKH≠∠BAC,故②错误,
∵∠BAF=∠ABC+∠C=2∠EBC+∠C,
∴∠BAF+∠C=2(∠EBC+∠C)=2∠BEF,故③正确,
∵∠BGH+∠DGH=180°,∠DGH+∠DEO=180°,
∴∠BGH=∠DEO=∠EBC+∠C=∠ABE+∠C,故④正确,
故答案为①③④
看了如图,△ABC中,BD、BE分...的网友还看了以下:
.“国家的实质是阶级统治的工具”属于()A.“君权神授论”观点B.“社会契约论”观点C.历史唯物主 2020-05-16 …
“社会形态的发展是一种自然历史过程”这是一种A 历史宿命论观点B 机械决定论观点C 历史唯心论 2020-06-04 …
1.“认识是主体对客体的直观反映”.这是一种()A.主观唯心主义认识论观点B.客观唯心主义认识论观 2020-06-05 …
“认识是主体对客体的直观反映”.这是一种()A.主观唯心主义认识论观点B.客观唯心主义认识论观点C 2020-06-05 …
“凡是真理都是客观的”这是A.唯物主义反映论观点B.形而上学观点C.唯心主义观点D.二元论观点 2020-07-14 …
“天行有常,不为尧存,不为桀亡”属于的观点?中国古代哲人荀子说“天行有常,不为尧存,不为桀亡”这是 2020-07-16 …
中国古代哲学家荀子说过.天行有尝,不为尧存,不为结忘.反映了()A.宿命论观点B.唯意志论观点C中 2020-07-16 …
中国古代哲人荀子说:“天行有常,不为尧存,不为桀亡.”这是一种A.宿命论观点B.唯意志论观点C.机 2020-07-29 …
“任何英雄人物的历史作用都不能超出他们所处历史条件所许可的范围”.这种观点属于?A、历史宿命论观点B 2020-11-03 …
"一切真知都发源于直接经验"是A唯心主义认识论观点B辨证唯物注意认识论观点C唯心主义经验论观点D古代 2020-12-23 …