早教吧作业答案频道 -->数学-->
在△ABC中,(1)如图1,BP为△ABC的角平分线,PM⊥AB于M,PN⊥BC于N,AB=50,BC=60请补全图形,并直接写出△ABP与△BPC面积的比值;(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和A
题目详情
在△ABC中,
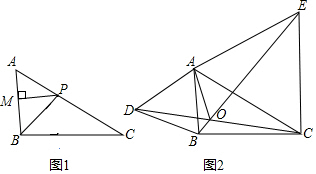
(1)如图1,BP为△ABC的角平分线,PM⊥AB于M,PN⊥BC于N,AB=50,BC=60请补全图形,并直接写出△ABP与△BPC面积的比值;
(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和ACE,CD与BE 相交于点O,求证:BE=CD;
(3)在(2)的条件下判断∠AOD与∠AOE的数量关系.(不需证明)

(1)如图1,BP为△ABC的角平分线,PM⊥AB于M,PN⊥BC于N,AB=50,BC=60请补全图形,并直接写出△ABP与△BPC面积的比值;
(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和ACE,CD与BE 相交于点O,求证:BE=CD;
(3)在(2)的条件下判断∠AOD与∠AOE的数量关系.(不需证明)
▼优质解答
答案和解析
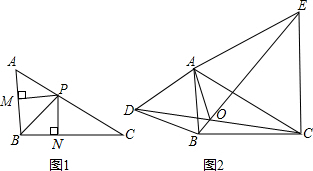 (1)如图1,作PN⊥BC于N,
(1)如图1,作PN⊥BC于N,
又∵BP为△ABC的角平分线,PM⊥AB于M,
∴PM=PN,
∴S△ABP:S△BPC=(
AB•PM):(
BC•PN)=AB:BC,
∵AB=50,BC=60,
∴△ABP与△BPC面积的比值为
;
(2)证明:如图2,∵△ABD和△ACE都是等边三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ABE和△ADC中,
,
∴△ABE≌△ADC(SAS),
∴BE=CD;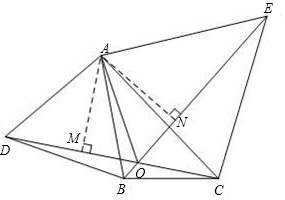
(3)∠AOD与∠AOE的数量关系为:∠AOD=∠AOE.
理由:如图,过点A作AM⊥DC于M,作AN⊥BE于N,
由(2)可得,△DAC≌△BAE,且DC=BE,
∴S△DAC=S△BAE,
即
×CD×AM=
×BE×AN,
∴AM=AN,
∴点A在∠DOE的角平分线上,
∴∠AOD=∠AOE.
 (1)如图1,作PN⊥BC于N,
(1)如图1,作PN⊥BC于N,又∵BP为△ABC的角平分线,PM⊥AB于M,
∴PM=PN,
∴S△ABP:S△BPC=(
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=50,BC=60,
∴△ABP与△BPC面积的比值为
| 5 |
| 6 |
(2)证明:如图2,∵△ABD和△ACE都是等边三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ABE和△ADC中,
|
∴△ABE≌△ADC(SAS),
∴BE=CD;

(3)∠AOD与∠AOE的数量关系为:∠AOD=∠AOE.
理由:如图,过点A作AM⊥DC于M,作AN⊥BE于N,
由(2)可得,△DAC≌△BAE,且DC=BE,
∴S△DAC=S△BAE,
即
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=AN,
∴点A在∠DOE的角平分线上,
∴∠AOD=∠AOE.
看了在△ABC中,(1)如图1,B...的网友还看了以下:
如果a的立方根与b的立方根的和的绝对值等于a的立方根的绝对值减去(b的立方根与ab的乘积)且不等于 2020-05-13 …
三角形ABC中,散影A的平方加扩散应B的平方加二倍散影A扩散应B等于0,三角形ABC是什么三角形A 2020-05-14 …
指出下列命题的互逆命题直角都相等内错角相等,两直线平行如果a+b大于0,那么a大于0,b大于0相等 2020-05-20 …
扇形圆心角的度数是[]A.大于0°B.大于0°,等于360°C.大于0°,小于360°D.任意度 2020-06-13 …
已知角α的终边上点p坐标A(a,b)关于X轴对称(a,b不等于0)角β的终边上的点Q与A关于直线y 2020-06-13 …
过椭圆x^2/a+y^2/b=1(a大于0,b大于0)的一个焦点是F(1,0),且与椭圆的短轴的两 2020-06-21 …
1、己知三角形ABC的三边a、b、c满足条件a²+b²+c²+338=10a+24b+2bc,试求 2020-07-19 …
白送分的题用“大于号”或“小于号”填空(1)、若a小于0,b小于0,则a+b()0;(2)、若a大 2020-08-01 …
下列叙述不正确的是A.若a大于0,b大于0,则ab大于0B.若a小于0,b小于0,ab大于0C.若a 2020-11-22 …
三角形的初步认识三角形ABC的三边长a,b,c都是正整数,且满足a大于0,b大于或等于a,c大于或等 2021-02-04 …