早教吧作业答案频道 -->数学-->
如图,点B、E、C、F在一条直线上,AB=DF,AC=DF,BE=FC.(1)求证:△ABC≌△DFE;(2)连接AF、BD,求证:四边形ABDF是平行四边形.
题目详情
如图,点B、E、C、F在一条直线上,AB=DF,AC=DF,BE=FC.
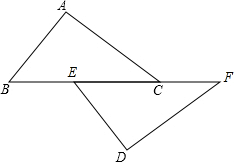
(1)求证:△ABC≌△DFE;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.

(1)求证:△ABC≌△DFE;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.
▼优质解答
答案和解析
证明:(1)∵BE=FC,
∴BC=EF,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SSS);
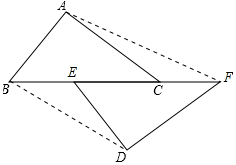
(2) 连接AF、BD,如图所示:
由(1)知△ABC≌△DFE,
∴∠ABC=∠DFE,
∴AB∥DF,
∵AB=DF,
∴四边形ABDF是平行四边形.
∴BC=EF,
在△ABC和△DFE中,
|

∴△ABC≌△DFE(SSS);
(2) 连接AF、BD,如图所示:
由(1)知△ABC≌△DFE,
∴∠ABC=∠DFE,
∴AB∥DF,
∵AB=DF,
∴四边形ABDF是平行四边形.
看了如图,点B、E、C、F在一条直...的网友还看了以下:
已知平面上三点如何求能组成平行四边形的另外一点?例如:已知A(a1,a2),B(b1,b2),C(c 2020-03-31 …
如图,在三角形ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形.求证四边形ADCE是 2020-04-05 …
在三角形ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形.求证:四边形ADCE是矩形 2020-04-05 …
难题,在等边△ABC中,点D是AC的中点,F是BC的中点,以BD为边作等边△BDE,求证:AB=E 2020-04-07 …
如图,梯形ABCD中,AB平行CD,E在AB上,CE//AD,且BE=CE,∠B=∠A+30°,求 2020-05-16 …
在如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为1 2020-05-16 …
初中平行四边形习题在三角行ABC中,角BCA=90`,点D,E分别是AC,AB边的中点.点F在BC 2020-05-21 …
①好学生②abcd×9=dcba③五个连续自然数的和是75,这五个+生学好求a()b()自然数分别 2020-05-22 …
初中相似几何题一道已知四边形ABCD∽四边形A'B'C'D',它们的周长分别为90cm,72cm, 2020-06-20 …
基于广度优先遍历可以求图中两个顶点间的:A.包含边数最多的路径B.任意一条路径C.包含边数最少的路 2020-07-09 …