早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连接CE、DF,CE与DF交于点O,求证:(1)CE=DF;(2)CE⊥DF.
题目详情
如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连接CE、DF,CE与DF交于点O,求证:
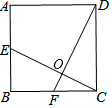
(1)CE=DF;
(2)CE⊥DF.

(1)CE=DF;
(2)CE⊥DF.
▼优质解答
答案和解析
证明:(1)∵四边形ABCD为正方形,
∴AB=BC=DC,∠ABC=∠FCD=90°,
∵E是边AB的中点,F是边BC的中点,
∴BE=
AB,FC=
BC,
∴BE=FC,
在△BEC和△CFD中,
∵
,
∴△BEC≌△CFD(SAS),
∴EC=DF;
(2)由(1)得:△BEC≌△CFD,
∴∠FDC=∠BCE,
∵∠FCD=90°,
∴∠DFC+∠FDC=90°,
∴∠DFC+∠BCE=90°,
∴∠FOC=90°,
∴CE⊥DF.
∴AB=BC=DC,∠ABC=∠FCD=90°,
∵E是边AB的中点,F是边BC的中点,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=FC,
在△BEC和△CFD中,
∵
|
∴△BEC≌△CFD(SAS),
∴EC=DF;
(2)由(1)得:△BEC≌△CFD,
∴∠FDC=∠BCE,
∵∠FCD=90°,
∴∠DFC+∠FDC=90°,
∴∠DFC+∠BCE=90°,
∴∠FOC=90°,
∴CE⊥DF.
看了如图,在正方形ABCD中,E是...的网友还看了以下:
如图所示,正方形ABCD的边长为6cm,点E为AB边上的一点,且AE=2cm,动点M由C点开始以3 2020-05-17 …
正方形ABCD的边长为12cm,连接AD边上任意一点F与BC边上任意一点G,再连接CE交AB于E, 2020-05-22 …
3条边相等的三角形叫做等边三角形,等边三角形的3个内角都是60度.(1)如图①,D,E为等边三角形 2020-06-06 …
三条边相等的三角形叫做等边三角形,等边三角形的三个内角都是60°(1)、如图一,D、E为等边三角形 2020-06-06 …
如图1,矩形BCD的边OD,OB分别在x轴和y轴上,且B(0,8),D(10,0).点E是DC边上 2020-06-19 …
已知三角形ABC中,AB=AC,D,E在三角形ABC中,AB=AC,点D,E是BC边上的点,将三角 2020-07-21 …
在等边三角形ABC中,E为直线AB上一点,连接EC.ED与直线BC交于点D,ED=EC.(1)如图 2020-07-30 …
如图所示,要测水池中一荷花E距岸边A和岸边D的距离.作法如下:(1)任作线段AB,取其中点O;(2) 2020-11-01 …
已知:等边△ABC中,当点D在BC边上,点E在AC边上,且BD=CE,连接AD、BE,交于点F,如图 2020-11-03 …
如图1,图2,在△ABC中,∠ACB=90°,AC=BC,AB=8,点D时AB边长的中点,点E时AB 2021-01-12 …