早教吧作业答案频道 -->数学-->
如图1,图2,在△ABC中,∠ACB=90°,AC=BC,AB=8,点D时AB边长的中点,点E时AB边上一动点(点E不与点A、B重合),连接CE,过点B作BF⊥CE于F,交射线CD于点G.(1)当点E在点D的左侧运动时,(图1
题目详情
如图1,图2,在△ABC中,∠ACB=90°,AC=BC,AB=8,点D时AB边长的中点,点E时AB边上一动点(点E不与点A、B重合),连接CE,过点B作BF⊥CE于F,交射线CD于点G.
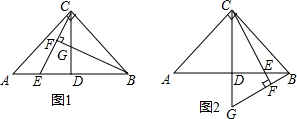
(1)当点E在点D的左侧运动时,(图1),求证:△ACE≌△CBG;
(2)当点E在点D的右侧运动时(图2),(1)中的结论是否成立?请说明理由;
(3)当点E运动到何处时,BG=5,试求出此时AE的长.
(1)当点E在点D的左侧运动时,(图1),求证:△ACE≌△CBG;
(2)当点E在点D的右侧运动时(图2),(1)中的结论是否成立?请说明理由;
(3)当点E运动到何处时,BG=5,试求出此时AE的长.

▼优质解答
答案和解析
(1)在Rt△ABC中,
∵AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,
,
∴△ACE≌△CBG;
(2)结论仍然成立,即△ACE≌△CBG.
理由如下:在Rt△ABC中,
∵AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
∴△ACE≌△CBG;
(3)在Rt△ABC中,
∵AC=BC,点D是AB的中点,
∴CD⊥AB,CD=AD=BD=
AB=4,
在Rt△BDG中,DG=
=3.
点E在运动的过程中,分两种情况讨论:
①当点E在点D的左侧运动时,CG=CD-DG=1,
∵△ACE≌△CBG,
∴AE=CG=1;
②当点E在点D的右侧运动时,CG=CD+DG=7,
∵△ACE≌△CBG,
∴AE=CG=7.
∵AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=
| 1 |
| 2 |
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,
|
∴△ACE≌△CBG;
(2)结论仍然成立,即△ACE≌△CBG.
理由如下:在Rt△ABC中,
∵AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=
| 1 |
| 2 |
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
∴△ACE≌△CBG;
(3)在Rt△ABC中,
∵AC=BC,点D是AB的中点,
∴CD⊥AB,CD=AD=BD=
| 1 |
| 2 |
在Rt△BDG中,DG=
| BG2-BD2 |
点E在运动的过程中,分两种情况讨论:
①当点E在点D的左侧运动时,CG=CD-DG=1,
∵△ACE≌△CBG,
∴AE=CG=1;
②当点E在点D的右侧运动时,CG=CD+DG=7,
∵△ACE≌△CBG,
∴AE=CG=7.
看了如图1,图2,在△ABC中,∠...的网友还看了以下:
已知P为正方形边BC上一点,BE垂直于AP,在AP延长线上取F,使EF=AE,连接BF,BC,求证 2020-05-17 …
AC为圆O的直径,B为半圆上一点,连接AB,BC,D为AC上一点,作DE=DB,交射线BC于点E, 2020-06-04 …
如图,在梯形ABCD中,AB∥CD,∠ABD=90°,AB=BD,在BC上截取BE,使BE=BA, 2020-06-12 …
如图,在三角形ABC中,角C等于2角B,D是BC上的一点,且AD垂直AB,点E是BD的中点,连接E 2020-06-27 …
如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将△BEC旋转,使点C落在BC上的点D处 2020-07-08 …
用遥控器设置电调,需要A.断开电机B.接上电机C.断开动力电源 2020-08-22 …
如图,要测量一个水潭的宽度,现由于不能直接测量,晓君是这样操作的:她在平地上选取一点C,该点可以直接 2020-11-02 …
有一池塘,要测的A,B两端的距离,设计了如下方案:如图,先在平地上取了一个可一个直接到达A,B的点C 2020-11-02 …
如图,在三棱柱...接上,三棱柱ABC-A'B'C'中,D为BC上一点,且A'B平行于平面AC'D. 2020-11-03 …
寝室有abcd四台电脑一个路由四台都能上网我的电脑f接上ad的线可以上网接上bc的闲就本地连接受限制 2020-11-21 …