早教吧作业答案频道 -->数学-->
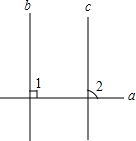
证明填空:如图,已知直线b∥c,a⊥b求证:a⊥c证明:∵a⊥b(已知)∴∠1=90°()又b∥c()∴∠1=∠2()∴∠2=∠1=90°()∴a⊥c()
题目详情
证明填空:如图,已知直线b∥c,a⊥b
求证:a⊥c
证明:∵a⊥b(已知)
∴∠1=90°(___ )
又b∥c(___ )
∴∠1=∠2(___ )
∴∠2=∠1=90°(___ )
∴a⊥c(___ )
求证:a⊥c
证明:∵a⊥b(已知)
∴∠1=90°(___ )
又b∥c(___ )
∴∠1=∠2(___ )
∴∠2=∠1=90°(___ )
∴a⊥c(___ )

▼优质解答
答案和解析
证明:∵a⊥b(已知)
∴∠1=90°(垂直的定义 )
又b∥c(已知 )
∴∠1=∠2(两直线平行,同位角相等 )
∴∠2=∠1=90°(等量代换 )
∴a⊥c(垂直的定义 ),
故答案为:垂直的定义,已知,两直线平行,同位角相等,等量代换,垂直的定义.
∴∠1=90°(垂直的定义 )
又b∥c(已知 )
∴∠1=∠2(两直线平行,同位角相等 )
∴∠2=∠1=90°(等量代换 )
∴a⊥c(垂直的定义 ),
故答案为:垂直的定义,已知,两直线平行,同位角相等,等量代换,垂直的定义.
看了证明填空:如图,已知直线b∥c...的网友还看了以下:
已知aΔb=(a-b)2,a※b=(a+b)(a-b),例如,1Δ2=(1-2)2=1,1※2=( 2020-05-15 …
已知A={1,2,a},B={1,a的二次方},A∪B={1,2,a},求所有可能的a值已知A={ 2020-06-02 …
已知(a+b)的2次方=9,(a-b)的2次方=1,求1.a的2次方+b的2次方=?2.ab=?3 2020-06-04 …
已知a+b+c=0,试求a^2/(2a^2+bc)+b^2/(2b^2+ac)+c^2/(2c^2 2020-06-11 …
1.已知a+b+c=0,a^2+b^2+c^=1,求:①ab+bc+ac的值②a^4+b^4+c^ 2020-07-09 …
初一化简求值4(x-y+z)-2(x+y-z)-3(-x-y-z).2(x2-2xy+y2-3)+ 2020-07-20 …
集合AB把集合{(a,b)|a属于A,b属于B}记作A×B,已知c={a}D-{1、2、3}求C× 2020-07-30 …
(a^4-2a^2b^2+b^4)÷(a+b)^2÷(a-b)已知(x^2-3x+4)(x^2-a 2020-08-03 …
已知1/m-1/n=1,求5m+7mn-5n/2n-3mn-2m的值计算(2)a/b-b/a-a^2 2020-11-01 …
已知a^2+b^2=5,ab=4求代数式5ab^2(a-b)-3ab(b-a)^2+5a^2b(b- 2020-11-20 …