早教吧作业答案频道 -->数学-->
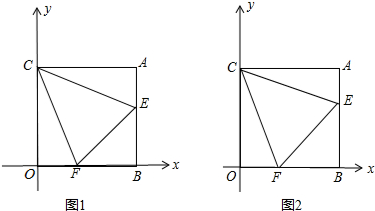
如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,m),A(n,m),且(m-4)2+n2-8n=-16,过C点作∠ECF分别交线段AB、OB于E、F两点.(1)求A点的坐标;(2)若OF+BE=AB,求证:CF
题目详情
如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,m),A(n,m),且(m-4)2+n2-8n=-16,过C点作∠ECF分别交线段AB、OB于E、F两点.
(1)求A点的坐标;
(2)若OF+BE=AB,求证:CF=CE;
(3)如图(2),若∠ECF=45°,求证:OF+AE=EF.
(1)求A点的坐标;
(2)若OF+BE=AB,求证:CF=CE;
(3)如图(2),若∠ECF=45°,求证:OF+AE=EF.

▼优质解答
答案和解析
(1)点A坐标满足,(m-4)2+n2-8n=-16,
整理得:(m-4)2+(n-4)2=0,
∴m=n=4,
∴点A坐标(4,4);
(2)∵OF+BE=AB,AE+BE=AB,
∴OF=AE,
∵CE=
,CF=
,AC=CO,
∴CF=CE;
(3)将△ACE顺时针旋转90°,则FG=AE+OF,CG=CE,
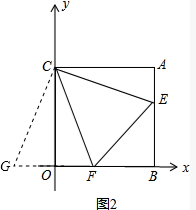
∵∠ECF=45°,
∴∠OCF+∠ACE=45°,∴∠GCF=45°,
在△GCF和△ECF中,
,
∴△GCF≌△ECF(SAS),
∴FG=EF,
∵FG=AE+OF,
∴EF=AE+OF.
整理得:(m-4)2+(n-4)2=0,
∴m=n=4,
∴点A坐标(4,4);
(2)∵OF+BE=AB,AE+BE=AB,
∴OF=AE,
∵CE=
| AC2+AE2 |
| OF2+OC2 |
∴CF=CE;
(3)将△ACE顺时针旋转90°,则FG=AE+OF,CG=CE,

∵∠ECF=45°,
∴∠OCF+∠ACE=45°,∴∠GCF=45°,
在△GCF和△ECF中,
|
∴△GCF≌△ECF(SAS),
∴FG=EF,
∵FG=AE+OF,
∴EF=AE+OF.
看了如图(1),在平面直角坐标系中...的网友还看了以下:
一道函数题,点M、N在第1象限,且在反比例函数Y=K/X(K大于0)的图象上,(M的横坐标比N小, 2020-04-26 …
证明C(0,n)^2+C(1,n)^2+……+C(n,n)^2=C(n,2n) 2020-04-26 …
已知:点A(m,2)和点B(2,n)都在反比例函数y=(m+3)/x的图像上.(1)求m与n的值; 2020-04-27 …
如图,△ABC经过某种变换得到的图形,点A与点P,点B与点Q,点C与点R是对应点,观察它们之间的关 2020-05-16 …
矩阵A,B,且AB=BA,怎么证明(A+B)^n=C(n,0)A^n+C(n,1)A^(n-1)B 2020-05-17 …
肽键的C--N键长、常规的C--N单键的长短问题?如题哪个长? 2020-05-24 …
一张桌子坐8人两张桌子并起来坐12人n张桌子可以坐多少人?32人需要多少张桌子 2020-06-03 …
一张桌子可以坐6人,两张桌子可以坐10人,n张桌子可以坐多少人 2020-06-04 …
赖氨酸R基为—C3H10N,则构成一个赖氨酸分子的C,N原子数分别为 2020-06-04 …
已知等差数列{an}的前n项的和为Sn,且S2=10,S5=55,则过点P(n,an)和Q(n+2 2020-06-07 …